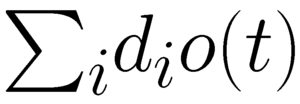If you aren't following my other blog, you just missed two fun posts trying to find some parametric curves. I'll try not to spam this blog too much with links to my other one. But I enjoyed these curves, and thought you might too.
Happy New Year!
Wednesday, December 31, 2008
Monday, December 29, 2008
Teaching Calc 2
Last semester I had the opportunity to teach Calc 2 here at the University of Virginia. And I get to this coming semester as well. While my course evaluations from last semester went well, there's still plenty of things I want to change. I thought I'd post some of my thoughts here, in hopes of maybe organizing them and, more importantly, getting some feedback.
First off, some parameters. I'm teaching out of Stewart's Calculus book, chapters 7 (Techniques of Integration), 8 (Applications - Arc Length and Surface Area), 10 (Parametric and Polar), 15 (Multiple Integrals), and then 11 (Series (Hurray!)). Yes, we skip the chapter on differential equations (in addition to some scattered sections), and chapter 15 might typically be considered Calc 3 material (that is, after all, where it is in the book). But the course I'm teaching is 'coordinated', meaning that there are several sections of it, and we all have common exams. This also means I'm to cover the above chapters in the order I list them in (or, I suppose, I could switch 7 and 8, or 10 and 15). I get to teach 3 times a week, for an hour each time. Finally, I have a TA who will be running an additional 'discussion section' (alternatively called a '4th hour'). Oh, and I expect to have approximately 40 students.
One of my concerns is finding how to best use my TA. The first (and only) time I had a TA, she got the usual duty (for calc classes here, anyway) of answering whatever questions the students had ("do this problem please") and giving a shortly weekly quiz. I didn't really like the plan, but had no idea what else to do. I still don't like the plan, and don't yet have much of a better plan on what to do. Besides perhaps not having the quiz during the discussion section itself, to save time (which I heard was a complaint among other classes last semester). When I have run my own discussion sections in the past, I haven't given a quiz at all.
So, some thoughts:
I'd also like to incorporate technology more. The classroom I'm teaching in has a computer and projector. I'm pretty sure (though I'll have to check) that the computers on campus (in labs and so forth) have Maple and/or Mathematica. I feel like this will help immensely in visualizing parametric and polar curves, and multiple integrals. Plus it gives me more fun things to play with :)
Oh, and I was also debating about making videos of me working through problems, and post them on youtube. I'm not exactly sure why (besides giving me an excuse to play with such things more). My students last semester did ask that I complete more problems during class, but I don't really feel like there's enough time. Plus, I'd rather have them finish up the problems. I like to only work the new parts of a problem, and let them finish up the algebra (or integrals using techniques from older sections). I certainly could write up the solutions (I do love LaTeX), but I wonder if the video approach might be more appreciated by students? Less intimidating, perhaps? Maybe I should have them make the videos? Or allow more freedom - let them make presentations posted online somewhere? Or not have them do any such thing, to avoid copyright worries and things?
First off, some parameters. I'm teaching out of Stewart's Calculus book, chapters 7 (Techniques of Integration), 8 (Applications - Arc Length and Surface Area), 10 (Parametric and Polar), 15 (Multiple Integrals), and then 11 (Series (Hurray!)). Yes, we skip the chapter on differential equations (in addition to some scattered sections), and chapter 15 might typically be considered Calc 3 material (that is, after all, where it is in the book). But the course I'm teaching is 'coordinated', meaning that there are several sections of it, and we all have common exams. This also means I'm to cover the above chapters in the order I list them in (or, I suppose, I could switch 7 and 8, or 10 and 15). I get to teach 3 times a week, for an hour each time. Finally, I have a TA who will be running an additional 'discussion section' (alternatively called a '4th hour'). Oh, and I expect to have approximately 40 students.
One of my concerns is finding how to best use my TA. The first (and only) time I had a TA, she got the usual duty (for calc classes here, anyway) of answering whatever questions the students had ("do this problem please") and giving a shortly weekly quiz. I didn't really like the plan, but had no idea what else to do. I still don't like the plan, and don't yet have much of a better plan on what to do. Besides perhaps not having the quiz during the discussion section itself, to save time (which I heard was a complaint among other classes last semester). When I have run my own discussion sections in the past, I haven't given a quiz at all.
So, some thoughts:
- Chapter 7, Techniques of Integration, is concerned with learning four techniques (and when they are mostly likely usefully applied). One thought I had was to break the class into four groups, and have each group teach one section (because you learn best when you teach). Of course, I'd meet with the groups and make suggestions and corrections and oversee to make sure things went mostly ok. Another idea I had, and might be leaning towards, is a bit more complicated. I thought I might write up a bunch of worked examples (some from the text, some solved problems, some examples from other texts) to distribute to the class along with a collection of unworked problems. I would not permit them to look at their book, at all, during this part of the class. Instead, the idea would be that they should look at the worked examples, try to find worked examples that look similar to the unworked problems, and learn their own way through the technique. I rather like this idea of 'pattern finding', which I like to think is part of what mathematics 'is' - as opposed to 'learn these mechanical procedures and repeat'. I may also structure the class so that each student presents a problem to the class. This might get them to start early so they can have more freedom in which problem they do (I'm thinking just ask for volunteers during each class, they get to work any problem that hasn't yet been done). It might also occupy some of the time in the first few discussion sections, which would be convenient.
- In Chapter 10, on parametric and polar equations, I thought I might give them a project: find parametric equations (likely piecewise, discontinuous) that will draw their initials. I'd probably allow piecewise linear functions, but would certainly encourage (5 points of the project for non-linearity?) something a bit smoother. This makes me wonder if it would be a bonus, extra credit project, or count as a weekly homework, or if I should also find some sort of similar project from each chapter (or for each of the exams?) so the course has somewhat more regularity (1 random project seems odd).
- I'm almost certain, though I distrust my memory, that in my calculus class as an undergraduate, we were given an assignment on a section before we ever talked about it in class. We were expected to go home, read the section, go to office hours if necessary (or work in groups), and complete problems from the section before the next class. I loved it. I have friends here in grad school that say they would have hated it. But I was thinking I might structure one chapter this way, perhaps chapter 8 (arc length and surface area). I recall last semester noticing that chapter 15 wasn't the most friendly read, but I wonder if chapter 8 might be better for that. I think if I do this I might pick the first couple of problems from each section and have them due at the beginning of class. These first few problems are typically pretty easy.
I'd also like to incorporate technology more. The classroom I'm teaching in has a computer and projector. I'm pretty sure (though I'll have to check) that the computers on campus (in labs and so forth) have Maple and/or Mathematica. I feel like this will help immensely in visualizing parametric and polar curves, and multiple integrals. Plus it gives me more fun things to play with :)
Oh, and I was also debating about making videos of me working through problems, and post them on youtube. I'm not exactly sure why (besides giving me an excuse to play with such things more). My students last semester did ask that I complete more problems during class, but I don't really feel like there's enough time. Plus, I'd rather have them finish up the problems. I like to only work the new parts of a problem, and let them finish up the algebra (or integrals using techniques from older sections). I certainly could write up the solutions (I do love LaTeX), but I wonder if the video approach might be more appreciated by students? Less intimidating, perhaps? Maybe I should have them make the videos? Or allow more freedom - let them make presentations posted online somewhere? Or not have them do any such thing, to avoid copyright worries and things?
Speed Limit Memory
I've got what I consider to be a poor memory. Or, at least, I try not to rely on it too much (perhaps that's why it's no good?). But anyway, I have a hard time remembering what the current speed limit is when driving. On my drive home yesterday from my holiday travels I got an idea for a helper. I was thinking, if you make a felt cover for the top half of your steering wheel (say), and indicated on it mileages from 25-65 in increments of 5, then with another felt ring you slide around to the appropriate place, you'd have a handy way to remember the speed limit. As long as you remember to update the position of the ring when you see a new speed limit sign, of course. I suggest felt, because it seems to me that two layers of felt might hold eachother together mostly, while still allowing some freedom of motion.
I dunno, maybe it's a poor idea. But as of right now, I like it. Plus when I tell my mom about it, it'll give her something fun to do (she sews, rather a lot).
Of course, it's only a temporary solution until the speed limit signs communicate wirelessly with a sensor in our cars that changes a heads-up display on the dashboard which always indicates the current speed limit. Unless, of course, self-driving cars come around before that, and the issue becomes moot.
I dunno, maybe it's a poor idea. But as of right now, I like it. Plus when I tell my mom about it, it'll give her something fun to do (she sews, rather a lot).
Of course, it's only a temporary solution until the speed limit signs communicate wirelessly with a sensor in our cars that changes a heads-up display on the dashboard which always indicates the current speed limit. Unless, of course, self-driving cars come around before that, and the issue becomes moot.
A Year of Running
Yeah, yeah, everybody is doing end of the year review posts, or posts looking forward to the next year. But I wanted to mess around with the Google Charts API, and figured my running mileage data was as good a data source as I'd find. So here's the chart I made with my monthly miles:
 The lightest blue indicates months with less than 100 miles run, and the one darkest (August) was the only month I passed 200 miles.
The lightest blue indicates months with less than 100 miles run, and the one darkest (August) was the only month I passed 200 miles.
Perhaps I should have waited through the next two days to post this, in case I decide to run. But even if I go both remaining days in December, I probably won't go more than 8 miles total. That won't affect my totals too much. Currently I've chalked up 1259 miles this year, occupying a little over 168 hours (= 1 full week). That puts my average pace at just slower than 8 minute miles. I thought about making another chart for my average pace each month, but don't feel like going through the computations. Another useless stat: I went for 178 runs, putting my average run length at just over 7 miles. That's an extra 250 miles and 28 runs over last year.
After August I was looking to crack 1500 miles this year, and was on pace for it. In September I ran my first 'ultra', though really the shortest ultra, a 50k. At that point, my running was looking pretty good, and I was thinking about a sub-3 hour marathon in Richmond in November, and doing a 50 mile run in the spring. However, my research was, as my advisor put it, 'stagnating'. Around the same time I met a girl (lucky me :)), and these factors put a 2 month halt in my running. I'm working on getting back into it, though still at a lesser volume. My current goal is the Charlottesville marathon in April, for my third consecutive year. I have no delusions of beating last year's 3:13, but I'm still hoping for sub-4 (had a 3:55 my first year). Guess we'll see.
Perhaps I should have waited through the next two days to post this, in case I decide to run. But even if I go both remaining days in December, I probably won't go more than 8 miles total. That won't affect my totals too much. Currently I've chalked up 1259 miles this year, occupying a little over 168 hours (= 1 full week). That puts my average pace at just slower than 8 minute miles. I thought about making another chart for my average pace each month, but don't feel like going through the computations. Another useless stat: I went for 178 runs, putting my average run length at just over 7 miles. That's an extra 250 miles and 28 runs over last year.
After August I was looking to crack 1500 miles this year, and was on pace for it. In September I ran my first 'ultra', though really the shortest ultra, a 50k. At that point, my running was looking pretty good, and I was thinking about a sub-3 hour marathon in Richmond in November, and doing a 50 mile run in the spring. However, my research was, as my advisor put it, 'stagnating'. Around the same time I met a girl (lucky me :)), and these factors put a 2 month halt in my running. I'm working on getting back into it, though still at a lesser volume. My current goal is the Charlottesville marathon in April, for my third consecutive year. I have no delusions of beating last year's 3:13, but I'm still hoping for sub-4 (had a 3:55 my first year). Guess we'll see.
Friday, December 12, 2008
Camera Box
Last weekend I bought a Nikon S550 digital camera (on sale at Staples for a little while still, if you were thinking about it). I've been having a good time taking pictures (and getting them off my camera from the command line using gphoto2, totally sweet). When I went to clean up my room a bit and recycle the box, I noticed that the box itself was also pretty cool. The box had a cardboard insert separator, which, when unfolded, looked like:
What's nice about that is with the cuts it has, and the folds, it folds up through a series of rigid motions (no folding/rolling except for on the pre-scored lines) to the following separator:
The whole box itself was also folded from a single unit, which lies flat (when unfolded):
And here they are together:
I don't know. Perhaps it's not that impressive. But I really liked it. No tape on the box, just lots of nice folding. As an origami fan, it appealed to me. Plus it gave me more excuses to take pictures, and play with Picasa.
What's nice about that is with the cuts it has, and the folds, it folds up through a series of rigid motions (no folding/rolling except for on the pre-scored lines) to the following separator:
The whole box itself was also folded from a single unit, which lies flat (when unfolded):
And here they are together:
I don't know. Perhaps it's not that impressive. But I really liked it. No tape on the box, just lots of nice folding. As an origami fan, it appealed to me. Plus it gave me more excuses to take pictures, and play with Picasa.
A Few Quotes
The other day on slashdot, the article "Twenty Years of Dijkstra's Cruelty" showed up. I was intruiged, and read the pdf it mentioned - a lovely handwritten paper by Dijkstra. I'm not a CS educator, so I don't have much to comment on about that aspect of the paper (the main point of it). However, I pulled two quotes out, and thought I'd share.
"... by developing a keen ear for unwarranted apologies, one can detect a lot of medieval thinking today."
"And when it comes to mathematics, you must realize that this is the human mind at an extreme limit of its capacity."
Tuesday, December 2, 2008
I'm 1!
Yep, my first post was one year ago today (though technically, I suppose, my first actual post was a week later). Four short months later I got my first comment, and two more months after that I'd had a visitor from every continent except Antarctica. I've gotten 60 comments (though nearly half of them are from me, responding), and had 125 posts. A post every 3 days, and a comment once a week... I'll take it. Especially because this blog tends to ramble and be pointless, even when it pretends to have something to say. All the same, it's been fun.
I thought I'd go back through and pick out my favorite posts so far. But then I couldn't decide what to link back to, and felt bad linking to myself. Most of my favorites were math posts, so you can find them here, because they were tagged. Perhaps my most useful post, if you live in or near Charlottesville anyway, was my writeup about the Rivanna Trail. According to my feedjit widget, this is also the most popular post (at least, from the past n days, I think that's how it works), followed closely by GPS in Ubuntu (which I find kinda surprising, but who am I to judge?). The post I wish more people had seen was this one, about a decent travel mug. I'm still interested to hear about a good travel mug (lid, in particular), especially now that it's almost gift-giving season :).
So, anyway, Happy Birthday blog! I'm a mostly proud parent. Don't get too jealous of your younger sibling (even if it does math better than you). For those following along, feel free to follow me on twitter, or my reader shared items, if you aren't already. I'd love to reciprocate.
I thought I'd go back through and pick out my favorite posts so far. But then I couldn't decide what to link back to, and felt bad linking to myself. Most of my favorites were math posts, so you can find them here, because they were tagged. Perhaps my most useful post, if you live in or near Charlottesville anyway, was my writeup about the Rivanna Trail. According to my feedjit widget, this is also the most popular post (at least, from the past n days, I think that's how it works), followed closely by GPS in Ubuntu (which I find kinda surprising, but who am I to judge?). The post I wish more people had seen was this one, about a decent travel mug. I'm still interested to hear about a good travel mug (lid, in particular), especially now that it's almost gift-giving season :).
So, anyway, Happy Birthday blog! I'm a mostly proud parent. Don't get too jealous of your younger sibling (even if it does math better than you). For those following along, feel free to follow me on twitter, or my reader shared items, if you aren't already. I'd love to reciprocate.
Sunday, November 30, 2008
A Teaching Statement
Such as it is, I have prepared a reflective (use caution in direct sunlight) teaching statement. I'm neither a deep thinker, nor a proficient writer, so I can't convince myself that the result is any good. Either way, here's what I came up with:
I have no idea why I bother teaching.
I can convince myself that many of my students will need to know mathematics in their future careers. My science students clearly need mathematics, but so do the business students. The fine arts are a little harder to justify, so perhaps pawn it off on "general education." Numeracy, people claim, is practically as important as literacy, even if it doesn't get the same attention (in fact, some people pride themselves on their innumeracy). If nothing else, mathematics courses are a requirement at the University, and I have enough of an understanding of the subject to try to get others through it.
So my issue with teaching isn't that the content isn't important.
My issue with teaching is that, in this connected age, there are effectively unlimited sources for the knowledge that I am supposed to cover in a calculus class. Certainly there has always been the textbook, and I love for my students to read it. But now, online, there are more places to learn calculus than one could possibly use. Entire lectures and individual problems and short snippets get posted as videos to YouTube. Wikipedia contains more information than any one person can know (and it's constantly growing!). I also must compete against the Massachusetts Institute of Technology, who not long ago started posting all course materials online (for free, accessible by anybody).
So why would a student bother coming to my class? Anything I'll be covering in class could be found online, from the relative comfort of a dorm room. It's not my job to tell students when to think about calculus, so I have no attendance policy. Who am I to tell them when they should be learning? If they are motivated enough to learn the material on their own, I don't want to frustrate their ambitions by making them come to class.
It is this sense of competition that drives my lectures. When planning lectures, I make sure to use examples that aren't covered in the book. I also try to find as many "fun" examples and extra problems as possible. Students don't necessarily want to look at other resources to learn the material I will be teaching. Even motivated students might not take that step. Students might not know where to look on Wikipedia for interesting mathematics that is, at the same time, easy enough to digest without having taken lots of math classes. It's my job to show these things to my students.
It's lucky, then, that mathematics is so fascinating. Surprising amounts can be boiled down and understood without having spent years taking math classes and reading math textbooks. This is my job. Anybody can present material, and cover examples. I think it is important to go further, to find more interesting examples, and historical tidbits. I always hope to show my students some of the beautiful things in mathematics.
During the times I am doing fun examples and presenting material that isn't strictly necessary for the class it is easy to be an excited speaker. However, there is something interesting to be found in nearly every example, and I try to keep my enthusiasm high throughout every lecture. Judging from course feedback, my students feed off this energy, and are more motivated to learn the material. If I can create motivated learners, who start seeing interesting things in the content I teach, then all of those external resources are more likely to be accessed and dug through. All the material in world is worth nothing if students aren't interested in looking at it. It is my hope that I can encourage some to embrace this interest.
I have no idea why I bother teaching.
I can convince myself that many of my students will need to know mathematics in their future careers. My science students clearly need mathematics, but so do the business students. The fine arts are a little harder to justify, so perhaps pawn it off on "general education." Numeracy, people claim, is practically as important as literacy, even if it doesn't get the same attention (in fact, some people pride themselves on their innumeracy). If nothing else, mathematics courses are a requirement at the University, and I have enough of an understanding of the subject to try to get others through it.
So my issue with teaching isn't that the content isn't important.
My issue with teaching is that, in this connected age, there are effectively unlimited sources for the knowledge that I am supposed to cover in a calculus class. Certainly there has always been the textbook, and I love for my students to read it. But now, online, there are more places to learn calculus than one could possibly use. Entire lectures and individual problems and short snippets get posted as videos to YouTube. Wikipedia contains more information than any one person can know (and it's constantly growing!). I also must compete against the Massachusetts Institute of Technology, who not long ago started posting all course materials online (for free, accessible by anybody).
So why would a student bother coming to my class? Anything I'll be covering in class could be found online, from the relative comfort of a dorm room. It's not my job to tell students when to think about calculus, so I have no attendance policy. Who am I to tell them when they should be learning? If they are motivated enough to learn the material on their own, I don't want to frustrate their ambitions by making them come to class.
It is this sense of competition that drives my lectures. When planning lectures, I make sure to use examples that aren't covered in the book. I also try to find as many "fun" examples and extra problems as possible. Students don't necessarily want to look at other resources to learn the material I will be teaching. Even motivated students might not take that step. Students might not know where to look on Wikipedia for interesting mathematics that is, at the same time, easy enough to digest without having taken lots of math classes. It's my job to show these things to my students.
It's lucky, then, that mathematics is so fascinating. Surprising amounts can be boiled down and understood without having spent years taking math classes and reading math textbooks. This is my job. Anybody can present material, and cover examples. I think it is important to go further, to find more interesting examples, and historical tidbits. I always hope to show my students some of the beautiful things in mathematics.
During the times I am doing fun examples and presenting material that isn't strictly necessary for the class it is easy to be an excited speaker. However, there is something interesting to be found in nearly every example, and I try to keep my enthusiasm high throughout every lecture. Judging from course feedback, my students feed off this energy, and are more motivated to learn the material. If I can create motivated learners, who start seeing interesting things in the content I teach, then all of those external resources are more likely to be accessed and dug through. All the material in world is worth nothing if students aren't interested in looking at it. It is my hope that I can encourage some to embrace this interest.
Thursday, November 27, 2008
Slackware!
I've been using Ubuntu for a while. It's got some great features, notably it's package management and update setup (which my friend has complained about, but I've always appreciated). But I've recently been frustrated with things responding slowly on my computer. I've tried turning off services and such, but it never seemed to improve. In the past, I've used gentoo and slackware, and I remembered them being a bit snappier for me. With a new version of slackware out, I thought it was about time to try something new(ish).
So I downloaded the iso images and burned them to cd. I backed up some data (been meaning to look at Amazon's S3 online storage... apparently that'll be another day though), and took the plunge. The setup seemed to be going well, until a failure when it got to installing mysql. Retry, and still fail. Took the disc out, tried cleaning it off, and still fail. So I came back to my ubuntu install, and found these directions about installing slackware without cds. I only skimmed through them, but got a good enough idea how things should go. Since the cds I had would properly boot and let me run setup, I think most of those directions weren't too necessary anyway. I downloaded new iso images, and rebooted with my install cd in the drive. When setup came around to asking for my source, I pointed it at the mount point (which I had made, and mounted things to before running setup) for my iso image, and was good to go.
One thing that confused me was that there are multiple install cds, but the directions at the link above didn't seem to care about that. They only indicated one disk. I mounted discs one and two in different locations, but I think you could save a step and mount both in the same place before running setup. I would have also mounted disc three, but it gave me an error about being able to find loop devices (perhaps I'm only allowed 2?). Anyway, after disc one was done, I was still in setup, and told it to install more packages from the second mount point. Seemed to go fine.
After a reboot, there was lilo, waiting for me. My ubuntu image wasn't there, but I've edited /etc/lilo.conf before, so I wasn't too concerned. First step: make a non-superuser - useradd. Next up, start the windowing environment (as pretty as the command line is) - startx. FAIL. "could not open default font 'fixed'", then "waiting for X server to begin accepting connections" and "giving up". That's not what I wanted to see.
Lynx, to google, and asked about it. This turned up, and using alt-F2 and alt-F1 to bounce between terminals, I got the commands entered. Fingers crossed, 'startx'... Hurray! Xfce.
Now I get to configure things again. Always a good time. I've got firefox 3 installed, and twitterfox, and the flash plugin, and my old bookmarks. I've got my desktop set back up basically the way I had it. That's probably enough for one day. Besides XEmacs and a terminal, that's pretty much all I use anyway. On that note, the default terminal isn't behaving at all for me. I type, and it doesn't even show the characters I type. I've been temporarily using xterm, but it's something I'll have to look at some more.
So I downloaded the iso images and burned them to cd. I backed up some data (been meaning to look at Amazon's S3 online storage... apparently that'll be another day though), and took the plunge. The setup seemed to be going well, until a failure when it got to installing mysql. Retry, and still fail. Took the disc out, tried cleaning it off, and still fail. So I came back to my ubuntu install, and found these directions about installing slackware without cds. I only skimmed through them, but got a good enough idea how things should go. Since the cds I had would properly boot and let me run setup, I think most of those directions weren't too necessary anyway. I downloaded new iso images, and rebooted with my install cd in the drive. When setup came around to asking for my source, I pointed it at the mount point (which I had made, and mounted things to before running setup) for my iso image, and was good to go.
One thing that confused me was that there are multiple install cds, but the directions at the link above didn't seem to care about that. They only indicated one disk. I mounted discs one and two in different locations, but I think you could save a step and mount both in the same place before running setup. I would have also mounted disc three, but it gave me an error about being able to find loop devices (perhaps I'm only allowed 2?). Anyway, after disc one was done, I was still in setup, and told it to install more packages from the second mount point. Seemed to go fine.
After a reboot, there was lilo, waiting for me. My ubuntu image wasn't there, but I've edited /etc/lilo.conf before, so I wasn't too concerned. First step: make a non-superuser - useradd. Next up, start the windowing environment (as pretty as the command line is) - startx. FAIL. "could not open default font 'fixed'", then "waiting for X server to begin accepting connections" and "giving up". That's not what I wanted to see.
Lynx, to google, and asked about it. This turned up, and using alt-F2 and alt-F1 to bounce between terminals, I got the commands entered. Fingers crossed, 'startx'... Hurray! Xfce.
Now I get to configure things again. Always a good time. I've got firefox 3 installed, and twitterfox, and the flash plugin, and my old bookmarks. I've got my desktop set back up basically the way I had it. That's probably enough for one day. Besides XEmacs and a terminal, that's pretty much all I use anyway. On that note, the default terminal isn't behaving at all for me. I type, and it doesn't even show the characters I type. I've been temporarily using xterm, but it's something I'll have to look at some more.
Wednesday, November 26, 2008
72 Pencils
I've been wanting to make my own copy of the 72 pencil sculpture by George W. Hart since I first saw it online. Have a look at it here, and explore his other works - they're awesome. I've had two boxes of 48 pencils sitting in my closet for a few years now, waiting for the day I was ready to make this thing. Yesterday I finally decided to make it, and went to Michael's to buy some styrofoam. I spent... probably 5 hours yesterday trying to work it out, and didn't get it. I woke up this morning, and stared at it for another 4 hours or so. Finally, I started over, and within about another hour I had it. Turns out, all of my first attempts had been started wrong. Idiot.
After I got it together:
 I thought I'd see what happened when I removed the rubber bands. Perhaps I removed them without enough care, but it ends up like this:
I thought I'd see what happened when I removed the rubber bands. Perhaps I removed them without enough care, but it ends up like this:

So I started over, taking pictures as I went. If you want to make your own, it really isn't that bad. I just wasn't being careful enough for my first... 10 tries or so :) What'll you need? 72 pencils (4 hexagonal cylinders, 18 pencils each) of course. I used a bit of styrofoam, a 1 inch think circular disc with diameter ~6 inches. To hold things together, I also used 4 pieces of string (each about a foot long, I'd guess) and 6 rubber bands. My cats wanted to help too:

I arranged the first 18 pencils in a cylinder poking into the styrofoam. The hexagon was bigger than it needed to be, and the pencils were wobbly, and not equally spaced. You might also notice
 that I put one rubber band around the styrofoam, which I did before any pencils were in. Next, start weaving some pencils into the uprights. You may find the original picture helpful. Here's a picture of the early stage of the process, for me:
that I put one rubber band around the styrofoam, which I did before any pencils were in. Next, start weaving some pencils into the uprights. You may find the original picture helpful. Here's a picture of the early stage of the process, for me:
 I have a couple of extra pencils (the black ones) in there for balance. They'll get removed later.
I have a couple of extra pencils (the black ones) in there for balance. They'll get removed later.
Keep stacking these pencils up, until it looks something like

After that, I tied a loop of string around each end of both horizontal cylinders. This permitted me to then put a rubber band around each end of the horizontal cylinders (and remove the strings)
 Now push the rubber band off the styrofoam base, to hold the bottom of the vertical cylinder. Put a rubber band around the top of the vertical cylinder, flip the whole thing over (so the styrofoam is up in the air), and pull the styrofoam off (which I found surprisingly easy). Now you've just got the forth cylinder to get in there. I had to follow the original picture, and carefully put pencils where they should be according to the picture. After the first few, it's pretty easy to see where they should go.
Now push the rubber band off the styrofoam base, to hold the bottom of the vertical cylinder. Put a rubber band around the top of the vertical cylinder, flip the whole thing over (so the styrofoam is up in the air), and pull the styrofoam off (which I found surprisingly easy). Now you've just got the forth cylinder to get in there. I had to follow the original picture, and carefully put pencils where they should be according to the picture. After the first few, it's pretty easy to see where they should go.
So, I don't know how helpful that was. It's really not too hard, as long as you start things correctly. This was my problem the first several times. But it all worked out in the end

 Of course, there's still those rubber bands. I'm not entirely sure how to get rid of them, so they'll probably stay for a while.
Of course, there's still those rubber bands. I'm not entirely sure how to get rid of them, so they'll probably stay for a while.
Update 20081201: Ok, with a little super glue one some obviously loose penciles, I was able to remove the rubber bands. Hoping it stays together for a while now.
After I got it together:
 I thought I'd see what happened when I removed the rubber bands. Perhaps I removed them without enough care, but it ends up like this:
I thought I'd see what happened when I removed the rubber bands. Perhaps I removed them without enough care, but it ends up like this:
So I started over, taking pictures as I went. If you want to make your own, it really isn't that bad. I just wasn't being careful enough for my first... 10 tries or so :) What'll you need? 72 pencils (4 hexagonal cylinders, 18 pencils each) of course. I used a bit of styrofoam, a 1 inch think circular disc with diameter ~6 inches. To hold things together, I also used 4 pieces of string (each about a foot long, I'd guess) and 6 rubber bands. My cats wanted to help too:

I arranged the first 18 pencils in a cylinder poking into the styrofoam. The hexagon was bigger than it needed to be, and the pencils were wobbly, and not equally spaced. You might also notice
 that I put one rubber band around the styrofoam, which I did before any pencils were in. Next, start weaving some pencils into the uprights. You may find the original picture helpful. Here's a picture of the early stage of the process, for me:
that I put one rubber band around the styrofoam, which I did before any pencils were in. Next, start weaving some pencils into the uprights. You may find the original picture helpful. Here's a picture of the early stage of the process, for me: I have a couple of extra pencils (the black ones) in there for balance. They'll get removed later.
I have a couple of extra pencils (the black ones) in there for balance. They'll get removed later.Keep stacking these pencils up, until it looks something like

After that, I tied a loop of string around each end of both horizontal cylinders. This permitted me to then put a rubber band around each end of the horizontal cylinders (and remove the strings)
 Now push the rubber band off the styrofoam base, to hold the bottom of the vertical cylinder. Put a rubber band around the top of the vertical cylinder, flip the whole thing over (so the styrofoam is up in the air), and pull the styrofoam off (which I found surprisingly easy). Now you've just got the forth cylinder to get in there. I had to follow the original picture, and carefully put pencils where they should be according to the picture. After the first few, it's pretty easy to see where they should go.
Now push the rubber band off the styrofoam base, to hold the bottom of the vertical cylinder. Put a rubber band around the top of the vertical cylinder, flip the whole thing over (so the styrofoam is up in the air), and pull the styrofoam off (which I found surprisingly easy). Now you've just got the forth cylinder to get in there. I had to follow the original picture, and carefully put pencils where they should be according to the picture. After the first few, it's pretty easy to see where they should go.So, I don't know how helpful that was. It's really not too hard, as long as you start things correctly. This was my problem the first several times. But it all worked out in the end

 Of course, there's still those rubber bands. I'm not entirely sure how to get rid of them, so they'll probably stay for a while.
Of course, there's still those rubber bands. I'm not entirely sure how to get rid of them, so they'll probably stay for a while.Update 20081201: Ok, with a little super glue one some obviously loose penciles, I was able to remove the rubber bands. Hoping it stays together for a while now.
Happy Thanksgiving
Yeah, yeah. I know I'm a day early. That's just how I'm making my Thanksgiving break work out. Anyway, I did some cooking, and thought I'd share.
First up, spiced fruit:
 It's a pretty easy recipe. Basically all you need is some canned fruit, some spices, and some butter. I used peaches, pears, pineapples, apricot halves, and black cherries. Empty the entire can (juice and all) of pineapples, and drained can of apricot halves and black cherries into a large oven-safe dish. Drain the juice from the peaches and pears into a separate dish, and put the fruit in the oven-safe dish. Use as much of the peach/pear juice as you'd like to fill up the main dish, and discard (or find some other way to use) the remaining juice. Next, add 1tsp cinnamon, and 1/2tsp nutmeg (my mom also uses 1tsp curry powder). Slice 1/2 stick of butter into pieces and set on top of the dish. Cook at 350 for 1 hour.
It's a pretty easy recipe. Basically all you need is some canned fruit, some spices, and some butter. I used peaches, pears, pineapples, apricot halves, and black cherries. Empty the entire can (juice and all) of pineapples, and drained can of apricot halves and black cherries into a large oven-safe dish. Drain the juice from the peaches and pears into a separate dish, and put the fruit in the oven-safe dish. Use as much of the peach/pear juice as you'd like to fill up the main dish, and discard (or find some other way to use) the remaining juice. Next, add 1tsp cinnamon, and 1/2tsp nutmeg (my mom also uses 1tsp curry powder). Slice 1/2 stick of butter into pieces and set on top of the dish. Cook at 350 for 1 hour.
Next up, apple and cranberry chicken skillet dish:
 This is basically the recipe here, with approx 5oz (I had a 10oz package, and used half) of dried cranberries instead of the onion.
This is basically the recipe here, with approx 5oz (I had a 10oz package, and used half) of dried cranberries instead of the onion.
Finally, pumpkin apple streusel cake:
 with some vanilla ice cream:
with some vanilla ice cream:
 following the recipe at epicurious.com.
following the recipe at epicurious.com.
I made some crescent rolls too, and will make some stuffing (with sausage!), and hot cider at some point. But these were the main dishes. OM NOM NOM.
Hope everybody has a nice Thanksgiving, and your cooking goes as well (better, actually - I gave myself a bit of a cut) as mine. Oh, and travelling, too - I'm happy I got to avoid that part.
First up, spiced fruit:
 It's a pretty easy recipe. Basically all you need is some canned fruit, some spices, and some butter. I used peaches, pears, pineapples, apricot halves, and black cherries. Empty the entire can (juice and all) of pineapples, and drained can of apricot halves and black cherries into a large oven-safe dish. Drain the juice from the peaches and pears into a separate dish, and put the fruit in the oven-safe dish. Use as much of the peach/pear juice as you'd like to fill up the main dish, and discard (or find some other way to use) the remaining juice. Next, add 1tsp cinnamon, and 1/2tsp nutmeg (my mom also uses 1tsp curry powder). Slice 1/2 stick of butter into pieces and set on top of the dish. Cook at 350 for 1 hour.
It's a pretty easy recipe. Basically all you need is some canned fruit, some spices, and some butter. I used peaches, pears, pineapples, apricot halves, and black cherries. Empty the entire can (juice and all) of pineapples, and drained can of apricot halves and black cherries into a large oven-safe dish. Drain the juice from the peaches and pears into a separate dish, and put the fruit in the oven-safe dish. Use as much of the peach/pear juice as you'd like to fill up the main dish, and discard (or find some other way to use) the remaining juice. Next, add 1tsp cinnamon, and 1/2tsp nutmeg (my mom also uses 1tsp curry powder). Slice 1/2 stick of butter into pieces and set on top of the dish. Cook at 350 for 1 hour.Next up, apple and cranberry chicken skillet dish:
 This is basically the recipe here, with approx 5oz (I had a 10oz package, and used half) of dried cranberries instead of the onion.
This is basically the recipe here, with approx 5oz (I had a 10oz package, and used half) of dried cranberries instead of the onion.Finally, pumpkin apple streusel cake:
 with some vanilla ice cream:
with some vanilla ice cream: following the recipe at epicurious.com.
following the recipe at epicurious.com.I made some crescent rolls too, and will make some stuffing (with sausage!), and hot cider at some point. But these were the main dishes. OM NOM NOM.
Hope everybody has a nice Thanksgiving, and your cooking goes as well (better, actually - I gave myself a bit of a cut) as mine. Oh, and travelling, too - I'm happy I got to avoid that part.
Saturday, November 22, 2008
Course Evaluations
With the end of the semester approaching, we've got course evaluations coming up. While the list of questions that every class gets its pretty decent, I like to add some more personalized questions to my evaluations. Currently what I've got is:
My questions for you: What do you look for in a course evaluation? What questions return the most meaningful answers for you, as an instructor? What questions, as a student, do you wish were asked?
Update 20081129: I thought up another question: Did you use any external sources to help you in this class? For example, books besides the textbook, or any websites? If so, what did you use, and to what extent?
- What feedback can you offer about the webwork system? Are there changes you would like to see, concerning the interface or features? How could it be made more useful for you?
- How did you feel about the combination of webwork and written homework? Did you feel they were fairly balanced?
- What parts of our course Collab page did you use, besides homework assignments? Did you look at homework or exam solutions? Did you follow any of the additional links under resources? In what ways do you wish Collab had been used differently?
- Were there certain topics or sections you felt were taught particularly well or particularly poorly?
- Is there anything you wish you would have been told about the class, before it started? What advice would you give to a future student of this course?
- What changes do you think Nick could make to improve this course?
My questions for you: What do you look for in a course evaluation? What questions return the most meaningful answers for you, as an instructor? What questions, as a student, do you wish were asked?
Update 20081129: I thought up another question: Did you use any external sources to help you in this class? For example, books besides the textbook, or any websites? If so, what did you use, and to what extent?
Monday, November 17, 2008
I Can Has Thesis?
No, I can't. Not for a while. Because I can't seem to figure out the things I'm supposed to be looking at, and because I distract myself by other things. One of the other distractions, recently, has been playing around with polynomials. If you've been following me here recently, you've seen this already. What you haven't seen is what's happened since then.
I decided to try out WordPress, because I knew it had good built-in support for LaTeX, which Blogger doesn't have. So, over at sumidiot.wordpress.com, I've been keeping a more regular log of the work I've been doing, which in the past few days has only been messing about with quartic and quadratic polynomials. And I think I'm about done with them. I have determined when a quartic can be decomposed, and what it's decompositions are. The final result seems to be that it is the composition of two quadratics iff it is symmetric around a vertical line. I won't redo all the equations and things, because they're already at the above pages.
So... I know that's not thesis quality work. It's probably something people have done before, and it took well under a week to work out. All the same, it's been the most independently motivated I've been by working on a math question since playing with FLT in high school (yes, I really did - and no (clearly) I didn't get anywhere). I've had a great time playing with this question, and I've still got more I'd like to look at. In the mean time, I really ought to be thinking about my actual research, which is, sadly, entirely unrelated.
I've also been trying to decide what to do with that wordpress account. The subtitle I've currently got up there indicates it might be a fork of this blog, for the mathematical content. I've debated about trying to use it regularly to just write up whatever I've been looking at - for research or for fun. Writing things up is good practice, and helps organize your thoughts. Both of these would probably be good for me. Do I drop this blogspot page? Or drop the wordpress one? Post weekly wrapup links from here to the wordpress page? Post wrapup links when some sort of progress has been made? I guess time will tell. I know you all can't wait to see what happens. I'll keep you posted. If Blogger would just natively support LaTeX...
I decided to try out WordPress, because I knew it had good built-in support for LaTeX, which Blogger doesn't have. So, over at sumidiot.wordpress.com, I've been keeping a more regular log of the work I've been doing, which in the past few days has only been messing about with quartic and quadratic polynomials. And I think I'm about done with them. I have determined when a quartic can be decomposed, and what it's decompositions are. The final result seems to be that it is the composition of two quadratics iff it is symmetric around a vertical line. I won't redo all the equations and things, because they're already at the above pages.
So... I know that's not thesis quality work. It's probably something people have done before, and it took well under a week to work out. All the same, it's been the most independently motivated I've been by working on a math question since playing with FLT in high school (yes, I really did - and no (clearly) I didn't get anywhere). I've had a great time playing with this question, and I've still got more I'd like to look at. In the mean time, I really ought to be thinking about my actual research, which is, sadly, entirely unrelated.
I've also been trying to decide what to do with that wordpress account. The subtitle I've currently got up there indicates it might be a fork of this blog, for the mathematical content. I've debated about trying to use it regularly to just write up whatever I've been looking at - for research or for fun. Writing things up is good practice, and helps organize your thoughts. Both of these would probably be good for me. Do I drop this blogspot page? Or drop the wordpress one? Post weekly wrapup links from here to the wordpress page? Post wrapup links when some sort of progress has been made? I guess time will tell. I know you all can't wait to see what happens. I'll keep you posted. If Blogger would just natively support LaTeX...
Wednesday, November 12, 2008
Quartics and Quadratics
I've been playing with polynomials a bit recently, and so I expect this post will be the first of several, explaining my explorations. The question I'd like to look at today is: When is a quartic (degree 4) polynomial the composite of two quadratics (degree 2)? Can every quartic be written as such a composite? Uniquely?
I wouldn't be surprised to find somebody has written this up before. In fact, they've probably dealt with more general questions, in an easier manner. All the same, this is how I spent my day, so I thought I'd share.
You might notice that 4 is the smallest degree polynomial that can be written as a composite of lower degree polynomials. If $p_i$ is a polynomial of degree $d_i$ (for $i=1,2$), then $p_1\circ p_2$ has degree $d_1\cdot d_2$. So if we wanted a cubic as a composite of lower degree polynomials, we'd have trouble doing it, and similarly for quadratics. However, these same considerations help us out a little bit. Suppose $f$ is a quartic that can be written as the composite $p_1\circ p_2$ of quadratics, and that T is a (non-constant) linear function. Then $T\circ f=T\circ p_1\circ p_2=(T\circ p_1)\circ p_2$, showing that $T\circ f$ is still the composite of two quadratics. The same argument works in reverse: if $T\circ f=p_1\circ p_2$, then $f=T^{-1}\circ p_1\circ p_2$ (and $T^{-1}$ exists, since $T$ was assumed linear), which is still the composite of quadratics.
What's the point of this linear function $T$? Well, suppose
Let $p_1=a_1x^2+b_1x+c_1$ and $p_2=a_2x^2+b_2x+c_2$. We'd like to know if we can write our $f$ above as $p_1\circ p_2$. If you're following along at home, I'll wait while you write out the composite $p_1\circ p_2$. To check your work (and mine), when you want $f=p_1\circ p_2$, you set the corresponding coefficients equal, and obtain the following system of equations:
Our simplifications let us write $a=1$ and $e=0$. Let's also go ahead and assume $a_1=a_2=1$ (that is, our quadratics are monic), to make our calculations easier. It's also believable (I hope) that we haven't lost anything with this assumption, but perhaps I should think about this some more. I had convinced myself of it in the office this afternoon. Anyway, this makes our equations
Remember that we're assuming $b$, $c$, and $d$ were fixed, and are hoping to find $b_1,b_2,c_1$, and $c_2$. The first line clearly makes it easy to find $b_2=b/2$, and we can substitute that in the remaining lines:
Now we're making progress. But first, we've made an assumption in the line $2d/b=2c_2+b_1$. What is it? Well, to divide by $b$, we assume $b\neq 0$. If, alternatively, $b=0$, then also $d=0$ (since $d$ is a multiple of $b$) and $b_2=0$. With all of these values being 0, the above system has 2 equations (the first and third) and 3 unknowns ($b_1$, $c_1$, and $c_2$). We can solve for $b_1$ and then $c_1$ in terms of a free variable $c_2$. Thus we obtain
Ok, so, assuming $b\neq 0$, what happens? The equations
Proposition: If $b\neq 0$ in the quartic $f=x^4+bx^3+cx^2+dx$, then $f$ can be written as the composite of quadratics only if $8d=4bc-b^3$ - in which case $f=p_1\circ p_2$ for
So there you have it. Not all quartics can be written as composites of quadratics. For those that can, there are a 1-parameter family of choices for monic quadratic factorizations.
Update 20081115: I've been thinking about my reduction that made the quadratics monic. I've been trying to decide if it was necessary. Playing around with the equations some more, it's not too hard to tell that you can't get rid of the relation $8d=4bc-b^3$ on the coefficients of the quartic, even if you don't assume your quadratics are monic. If you allow non-monic quadratics (but still want the composition to be monic), you have a free choice of value for $a_1$ (as long as it's positive) and for $c_2$ still, and the other coefficients can be solved for in terms of these two values (and the coefficients for the quartic).
Also, the two propositions could be combined. The relation $8d=4bc-b^3$ is present in both propositions, and there's no reason to assume $b\neq 0$ in that relation. Of course, we do end up dividing by $b$ to solve for coefficients in $p_1$ and $p_2$, so it's something to keep in mind.
Ok, I better go do some real work. I've still got other polynomial questions to look at, but they'll have to wait.
I wouldn't be surprised to find somebody has written this up before. In fact, they've probably dealt with more general questions, in an easier manner. All the same, this is how I spent my day, so I thought I'd share.
You might notice that 4 is the smallest degree polynomial that can be written as a composite of lower degree polynomials. If $p_i$ is a polynomial of degree $d_i$ (for $i=1,2$), then $p_1\circ p_2$ has degree $d_1\cdot d_2$. So if we wanted a cubic as a composite of lower degree polynomials, we'd have trouble doing it, and similarly for quadratics. However, these same considerations help us out a little bit. Suppose $f$ is a quartic that can be written as the composite $p_1\circ p_2$ of quadratics, and that T is a (non-constant) linear function. Then $T\circ f=T\circ p_1\circ p_2=(T\circ p_1)\circ p_2$, showing that $T\circ f$ is still the composite of two quadratics. The same argument works in reverse: if $T\circ f=p_1\circ p_2$, then $f=T^{-1}\circ p_1\circ p_2$ (and $T^{-1}$ exists, since $T$ was assumed linear), which is still the composite of quadratics.
What's the point of this linear function $T$? Well, suppose
$f=ax^4+bx^3+cx^2+dx+e.$
Let $T=\frac{1}{a}(x-e)$, and then notice that $T\circ f$ is monic (leading coefficient 1) and has 0 constant term. If the polynomial $T\circ f$ can be written as a composition of quadratics, then by the previous paragraph, $f$ can be written similarly. So, we can make our lives easier, and assume that $a=1$ and $e=0$.Let $p_1=a_1x^2+b_1x+c_1$ and $p_2=a_2x^2+b_2x+c_2$. We'd like to know if we can write our $f$ above as $p_1\circ p_2$. If you're following along at home, I'll wait while you write out the composite $p_1\circ p_2$. To check your work (and mine), when you want $f=p_1\circ p_2$, you set the corresponding coefficients equal, and obtain the following system of equations:
$a=a_1a_2^2$
$b=2a_1a_2b_2$
$c=2a_1a_2c_2+a_1b_2^2+a_2b_1$
$d=2a_1b_2c_2+b_1b_2$
$e=a_1c_2^2+b_1c_2+c_1$
$b=2a_1a_2b_2$
$c=2a_1a_2c_2+a_1b_2^2+a_2b_1$
$d=2a_1b_2c_2+b_1b_2$
$e=a_1c_2^2+b_1c_2+c_1$
Our simplifications let us write $a=1$ and $e=0$. Let's also go ahead and assume $a_1=a_2=1$ (that is, our quadratics are monic), to make our calculations easier. It's also believable (I hope) that we haven't lost anything with this assumption, but perhaps I should think about this some more. I had convinced myself of it in the office this afternoon. Anyway, this makes our equations
$b=2b_2$
$c=2c_2+b_2^2+b_1$
$d=2b_2c_2+b_1b_2$
$0=c_2^2+b_1c_2+c_1$
$c=2c_2+b_2^2+b_1$
$d=2b_2c_2+b_1b_2$
$0=c_2^2+b_1c_2+c_1$
Remember that we're assuming $b$, $c$, and $d$ were fixed, and are hoping to find $b_1,b_2,c_1$, and $c_2$. The first line clearly makes it easy to find $b_2=b/2$, and we can substitute that in the remaining lines:
$c=2c_2+b_1+(b^2/4)$, or $c-b^2/4=2c_2+b_1$
$d=(b/2)(2c_2+b_1)$, or $2d/b=2c_2+b_1$
$0=c_2^2+b_1c_2+c_1$
$d=(b/2)(2c_2+b_1)$, or $2d/b=2c_2+b_1$
$0=c_2^2+b_1c_2+c_1$
Now we're making progress. But first, we've made an assumption in the line $2d/b=2c_2+b_1$. What is it? Well, to divide by $b$, we assume $b\neq 0$. If, alternatively, $b=0$, then also $d=0$ (since $d$ is a multiple of $b$) and $b_2=0$. With all of these values being 0, the above system has 2 equations (the first and third) and 3 unknowns ($b_1$, $c_1$, and $c_2$). We can solve for $b_1$ and then $c_1$ in terms of a free variable $c_2$. Thus we obtain
Proposition: A quartic $x^4+cx^2+dx$ with $d\neq 0$ can not be written as the composition of two quadratics. The quartic $x^4+cx^2$ can be written as the composite $p_1\circ p_2$ where
$p_1=x^2+(c-2c_2)x+(c_2^2-cc_2)$
$p_2=x^2+c_2$
and $c_2$ can be any value.$p_2=x^2+c_2$
Ok, so, assuming $b\neq 0$, what happens? The equations
$c-b^2/4=2c_2+b_1$
$2d/b=2c_2+b_1$
mean that $c-b^2/4=2d/b$, which we chose to re-write as $8d=4bc-b^3$. This is a requirement on the coefficients of the original quartic. However, if this is satisfied, then we can pick$2d/b=2c_2+b_1$
$b_1=2d/b-2c_2$
$c_1=c_2^2-2dc_2/b$
in terms of a free variable $c_2$. We conclude by stating the final proposition, which can be checked by brute force (like everything else above):$c_1=c_2^2-2dc_2/b$
Proposition: If $b\neq 0$ in the quartic $f=x^4+bx^3+cx^2+dx$, then $f$ can be written as the composite of quadratics only if $8d=4bc-b^3$ - in which case $f=p_1\circ p_2$ for
$p_1=x^2+(2d/b-2c_2)x+(c_2^2-2dc_2/b)$
$p_2=x^2+b/2 x+c_2$
where $c_2$ can be any value.$p_2=x^2+b/2 x+c_2$
So there you have it. Not all quartics can be written as composites of quadratics. For those that can, there are a 1-parameter family of choices for monic quadratic factorizations.
Update 20081115: I've been thinking about my reduction that made the quadratics monic. I've been trying to decide if it was necessary. Playing around with the equations some more, it's not too hard to tell that you can't get rid of the relation $8d=4bc-b^3$ on the coefficients of the quartic, even if you don't assume your quadratics are monic. If you allow non-monic quadratics (but still want the composition to be monic), you have a free choice of value for $a_1$ (as long as it's positive) and for $c_2$ still, and the other coefficients can be solved for in terms of these two values (and the coefficients for the quartic).
Also, the two propositions could be combined. The relation $8d=4bc-b^3$ is present in both propositions, and there's no reason to assume $b\neq 0$ in that relation. Of course, we do end up dividing by $b$ to solve for coefficients in $p_1$ and $p_2$, so it's something to keep in mind.
Ok, I better go do some real work. I've still got other polynomial questions to look at, but they'll have to wait.
Sunday, November 9, 2008
A Fun Category
During my time in grad school, I have often wondered what I would talk about if I were invited to give a talk to an undergraduate audience. Like the math club here, or where I went for undergrad. I've generally had a good time with categories, and am pretty convinced something like the following would work as a fun talk. Perhaps my definition of fun needs some work.
For starters, let's just think about sets for a while - and I'll have finite sets in mind, but mostly that shouldn't matter. If $S$ and $T$ are sets, the Cartesian product is the set $S\times T=\{(s,t)|s\in S,t\in T\}$. What makes this new set useful? Why should we care about it? I suppose it depends on who you ask, but since I've got categories in mind, I want to think about functions (=maps) between sets. The product comes with 2 maps, I'll call them $\pi_S$ and $\pi_T$. The map $\pi_S:S\times T\to S$ is defined by $(s,t)\mapsto s$, and the map $\pi_T$ is similar. Now, if I have a set $A$, and a map $f:A\to S\times T$, then I can compose $f$ with either $\pi_S$ or $\pi_T$ and obtain maps $\pi_S\circ f:A\to S$ and $\pi_T\circ f:A\to T$. That is, I can tease out the component pieces of the map $f$. On the other hand, if I started with a set $B$, and maps $g:B\to S$ and $h:B\to T$, I can define a map $(g,h):B\to S\times T$ via $b\mapsto (g(b),h(b))$.
So when I think about the product of two sets, I notice that maps to the product are essentially the same as individual maps to the sets I started with. This is how I want to think about the product in other contexts. If I start with two things (objects in some category) $x$ and $y$, I want their product $x\times y$ to be another thing (object) with the property that whenever I have component maps (a map to $x$ and a map to $y$), then I get a map to the product. Additionally, my product will come with two maps, $\pi_x$ and $\pi_y$, which I think of as the projections, following the example above.
What I'd like to do now is pick a fun context (category) and figure out what the product is in that category. In a category I'm supposed to have some collection of objects, and some collection of arrows between objects (satisfying various properties). So the category of finite sets, that I used above, just had finite sets as objects and functions as arrows. My new category will have as objects the positive integers. There will be a single arrow from $n$ to $m$ precisely when $n$ divides $m$.
So what is the product of $n$ and $m$ in this category? For now, let me call it $p$. Remember that $p$ comes with maps to $n$ and $m$ - which is to say, $p$ divides $n$ and $m$. There's a word for that - $p$ is a common divisor of $n$ and $m$. Which common divisor? Well, suppose $a$ is some other divisor. That means $a$ divides $n$ and $m$, or, in arrow notation, $a\to n$ and $a\to m$. But part of being the product was that whenever I have maps to $n$ and $m$, I get a map to the product, $p$. So $a\to p$, or, in other words, $a$ divides $p$. So, we've found that if $a$ is any other divisor of $n$ and $m$, then since $p$ is the product, $a$ must divide $p$. That makes $p$ the greatest common divisor.
Wasn't that fun?
These things can be 'dualized', and what you get is supposed to be called the sum. 'Dualizing' means flipping all the arrows around. Let's go back to finite sets for a minute. The product $S\times T$ came with maps $S\times T\to S$ and $S\times T\to T$. The dual of this idea (call it the coproduct, or sum), is an object, which I'll denote $S\coprod T$ and it has arrows $S\to S\coprod T$ and $T\to S\coprod T$. Notice how the arrows are going the 'other way' than they did for the product? For the product we mapped from the product to the components, whereas for the sum we map from the components to the sum. The sum also has the property that if $S\to A$ and $T\to A$, then $S\coprod T\to A$ (again, notice how this is flipped from the product case, where $A\to S$ and $A\to T$ gave $A\to S\times T$). The object, in sets, that is the coproduct is more commonly known as the disjoint union.
Exercise for the reader: what is the coproduct in the other category above, the 'divides' category?
You might ask why I decided that what was important, back in the beginning, was functions (maps). It's a good question. I've read somewhere (though I forget where) that thinking about objects by themselves is ok, but thinking about how they related to other objects (via maps) is even better. For a while I wasn't really sure why this should be, but I'm starting to put it together. If you go back and think about set cardinalities, you'll quickly notice that you are really asking about maps between sets, as a way to compare their sizes. If there is an injective or surjective map, you know one of the objects is at least as big as the other. If you've got a bijection, the two sets are the same size. It's hard to think about the size of a set, once you get past finite sets (but even there, really), without comparing it to other sets. And the way you compare sets is via maps between them. For an somewhat more advanced example, algebraic topology is wholly dedicated to maps between spaces. If you've got some space $X$, you decide that you'd really like to know about maps from various dimensional spheres into your space $X$. But perhaps that's a subject for another day.
For starters, let's just think about sets for a while - and I'll have finite sets in mind, but mostly that shouldn't matter. If $S$ and $T$ are sets, the Cartesian product is the set $S\times T=\{(s,t)|s\in S,t\in T\}$. What makes this new set useful? Why should we care about it? I suppose it depends on who you ask, but since I've got categories in mind, I want to think about functions (=maps) between sets. The product comes with 2 maps, I'll call them $\pi_S$ and $\pi_T$. The map $\pi_S:S\times T\to S$ is defined by $(s,t)\mapsto s$, and the map $\pi_T$ is similar. Now, if I have a set $A$, and a map $f:A\to S\times T$, then I can compose $f$ with either $\pi_S$ or $\pi_T$ and obtain maps $\pi_S\circ f:A\to S$ and $\pi_T\circ f:A\to T$. That is, I can tease out the component pieces of the map $f$. On the other hand, if I started with a set $B$, and maps $g:B\to S$ and $h:B\to T$, I can define a map $(g,h):B\to S\times T$ via $b\mapsto (g(b),h(b))$.
So when I think about the product of two sets, I notice that maps to the product are essentially the same as individual maps to the sets I started with. This is how I want to think about the product in other contexts. If I start with two things (objects in some category) $x$ and $y$, I want their product $x\times y$ to be another thing (object) with the property that whenever I have component maps (a map to $x$ and a map to $y$), then I get a map to the product. Additionally, my product will come with two maps, $\pi_x$ and $\pi_y$, which I think of as the projections, following the example above.
What I'd like to do now is pick a fun context (category) and figure out what the product is in that category. In a category I'm supposed to have some collection of objects, and some collection of arrows between objects (satisfying various properties). So the category of finite sets, that I used above, just had finite sets as objects and functions as arrows. My new category will have as objects the positive integers. There will be a single arrow from $n$ to $m$ precisely when $n$ divides $m$.
So what is the product of $n$ and $m$ in this category? For now, let me call it $p$. Remember that $p$ comes with maps to $n$ and $m$ - which is to say, $p$ divides $n$ and $m$. There's a word for that - $p$ is a common divisor of $n$ and $m$. Which common divisor? Well, suppose $a$ is some other divisor. That means $a$ divides $n$ and $m$, or, in arrow notation, $a\to n$ and $a\to m$. But part of being the product was that whenever I have maps to $n$ and $m$, I get a map to the product, $p$. So $a\to p$, or, in other words, $a$ divides $p$. So, we've found that if $a$ is any other divisor of $n$ and $m$, then since $p$ is the product, $a$ must divide $p$. That makes $p$ the greatest common divisor.
Wasn't that fun?
These things can be 'dualized', and what you get is supposed to be called the sum. 'Dualizing' means flipping all the arrows around. Let's go back to finite sets for a minute. The product $S\times T$ came with maps $S\times T\to S$ and $S\times T\to T$. The dual of this idea (call it the coproduct, or sum), is an object, which I'll denote $S\coprod T$ and it has arrows $S\to S\coprod T$ and $T\to S\coprod T$. Notice how the arrows are going the 'other way' than they did for the product? For the product we mapped from the product to the components, whereas for the sum we map from the components to the sum. The sum also has the property that if $S\to A$ and $T\to A$, then $S\coprod T\to A$ (again, notice how this is flipped from the product case, where $A\to S$ and $A\to T$ gave $A\to S\times T$). The object, in sets, that is the coproduct is more commonly known as the disjoint union.
Exercise for the reader: what is the coproduct in the other category above, the 'divides' category?
You might ask why I decided that what was important, back in the beginning, was functions (maps). It's a good question. I've read somewhere (though I forget where) that thinking about objects by themselves is ok, but thinking about how they related to other objects (via maps) is even better. For a while I wasn't really sure why this should be, but I'm starting to put it together. If you go back and think about set cardinalities, you'll quickly notice that you are really asking about maps between sets, as a way to compare their sizes. If there is an injective or surjective map, you know one of the objects is at least as big as the other. If you've got a bijection, the two sets are the same size. It's hard to think about the size of a set, once you get past finite sets (but even there, really), without comparing it to other sets. And the way you compare sets is via maps between them. For an somewhat more advanced example, algebraic topology is wholly dedicated to maps between spaces. If you've got some space $X$, you decide that you'd really like to know about maps from various dimensional spheres into your space $X$. But perhaps that's a subject for another day.
Sunday, November 2, 2008
Fun with Series
The 'Sequences and Series' chapter of Calc 2 is the one I have been looking forward to the most, because there are some many awesome external diversions one can bring in to the class. I've already talked here about the first batch of fun things I mentioned in class, and thought I might update on some more things I've said, and plan on saying.
Now that we've talked about geometric series, it's possible to compute the area of the Koch snowflake, whose length we already computed in class when we talked about sequences. Our text (Stewart) has an exercise about the Cantor set, and the Sierpinski Carpet. The students are asked to compute the total length removed from [0,1] in order to make the Cantor set, and similarly the area removed to make Sierpinski's Carpet. I hope they found it surprising that the bits removed had the same length as the interval, and area as the square, even though there are still (clearly) infinitely many points remaining. While I was at it, I mentioned the Menger Sponge origami projects (and looking them up again convinced me that I should probably do one someday).
Though I've not yet figured out how, exactly, to bring it up in class, I think we're going to have a day and talk about cardinalities a little. I should at least show them that there is more than one infinity. Clearly it ties in to the examples from the previous paragraph, but it's also just good for their general education. Plus it's hugely fascinating. And they've spent all this time thinking about functions on the real line, they might as well know a little more about the line itself.
Even though I don't know a whole lot about it, since we were talking about p-series the other day I figured I should mention Riemann's ζ function, the associated Hypothesis, and the million dollar reward for a proof. They seemed to enjoy that there was a financial incentive, but at least one commented that there were surely easier ways to make a million dollars. I also showed how the divergence of the harmonic series implies that there are infinitely many primes, by considering the expression
We also talked about the integral test in class, so I couldn't help bringing up the Euler-Mascheroni constant γ. I didn't say horribly much about it in class, but did mention how it can be used to approximate the number of terms in the harmonic series you would have to add up in order to get a chosen value. I worked through determining that it requires more than 12000 terms to just add up to 100.
The next thing I plan on talking about in class is sometimes referred to as the Kempner Series, and is obtained from the harmonic series by removing those terms whose denominators have some chosen digit. For example, remove all the terms that have a 0 as a digit in the denominator. What is initially surprising about this series is that it converges, though after some more thought you realize you've thrown out rather a lot of the series. Anyway, to show the Kempner series converges, you compare against a geometric series - all things we're talking about in my class.
Perhaps some of the most fun (besides, perhaps, the multiple infinities) will be once we get to Taylor series. I plan on presenting one of Euler's proofs that $\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$, by thinking about the Taylor series for $\sin(x)/x$. The way this works is to realize that $\sin(x)/x$ is zero at the non-zero integer multiples of $\pi$, so you think of the infinite polynomial that is the Taylor series as also being the product $\prod_{0\neq n}(1-x/(n\pi))$. After expanding this infinite product, you compare the coefficient of $x^2$ to the corresponding coefficient from the Taylor series, and Robert's your father's brother.
Another fun example I plan on doing (at least to some extent) is showing that
The final fun thing about Taylor series is it gives a nice segway into my research. Of course, I won't get too involved with telling them about my research, exactly. But I will mention that it's a direct analogy to Taylor series. And it'll give me a chance to talk about topology, which is always good.
Update 20081103: I realized I should include some text references here, sorry about that. The two books I had in mind were:
Now that we've talked about geometric series, it's possible to compute the area of the Koch snowflake, whose length we already computed in class when we talked about sequences. Our text (Stewart) has an exercise about the Cantor set, and the Sierpinski Carpet. The students are asked to compute the total length removed from [0,1] in order to make the Cantor set, and similarly the area removed to make Sierpinski's Carpet. I hope they found it surprising that the bits removed had the same length as the interval, and area as the square, even though there are still (clearly) infinitely many points remaining. While I was at it, I mentioned the Menger Sponge origami projects (and looking them up again convinced me that I should probably do one someday).
Though I've not yet figured out how, exactly, to bring it up in class, I think we're going to have a day and talk about cardinalities a little. I should at least show them that there is more than one infinity. Clearly it ties in to the examples from the previous paragraph, but it's also just good for their general education. Plus it's hugely fascinating. And they've spent all this time thinking about functions on the real line, they might as well know a little more about the line itself.
Even though I don't know a whole lot about it, since we were talking about p-series the other day I figured I should mention Riemann's ζ function, the associated Hypothesis, and the million dollar reward for a proof. They seemed to enjoy that there was a financial incentive, but at least one commented that there were surely easier ways to make a million dollars. I also showed how the divergence of the harmonic series implies that there are infinitely many primes, by considering the expression
$\sum_{n=1}^{\infty}\frac{1}{n}=\prod_{p}\frac{1}{1-p^{-1}}=\prod_{p}\left(\sum_{k=0}^{\infty} 1/p^k\right)$
These products are taken over all primes.
We also talked about the integral test in class, so I couldn't help bringing up the Euler-Mascheroni constant γ. I didn't say horribly much about it in class, but did mention how it can be used to approximate the number of terms in the harmonic series you would have to add up in order to get a chosen value. I worked through determining that it requires more than 12000 terms to just add up to 100.
The next thing I plan on talking about in class is sometimes referred to as the Kempner Series, and is obtained from the harmonic series by removing those terms whose denominators have some chosen digit. For example, remove all the terms that have a 0 as a digit in the denominator. What is initially surprising about this series is that it converges, though after some more thought you realize you've thrown out rather a lot of the series. Anyway, to show the Kempner series converges, you compare against a geometric series - all things we're talking about in my class.
Perhaps some of the most fun (besides, perhaps, the multiple infinities) will be once we get to Taylor series. I plan on presenting one of Euler's proofs that $\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$, by thinking about the Taylor series for $\sin(x)/x$. The way this works is to realize that $\sin(x)/x$ is zero at the non-zero integer multiples of $\pi$, so you think of the infinite polynomial that is the Taylor series as also being the product $\prod_{0\neq n}(1-x/(n\pi))$. After expanding this infinite product, you compare the coefficient of $x^2$ to the corresponding coefficient from the Taylor series, and Robert's your father's brother.
Another fun example I plan on doing (at least to some extent) is showing that
$\int_0^1 \frac{1}{x^x}dx=\sum_{n=1}^{\infty}\frac{1}{x^x}.$
This requires a bit of messing about, but it's so pretty that it's got to be worth it, right?The final fun thing about Taylor series is it gives a nice segway into my research. Of course, I won't get too involved with telling them about my research, exactly. But I will mention that it's a direct analogy to Taylor series. And it'll give me a chance to talk about topology, which is always good.
Update 20081103: I realized I should include some text references here, sorry about that. The two books I had in mind were:
Thursday, October 23, 2008
Fun with Sequences
We started the chapter on Sequences and Series in my calc II class last week. This is the chapter I have been looking forward to the most, even though, of course, all of the chapters are interesting. I decided to use one class period mostly talking about things that didn't matter for the class at all, because they are irresistibly fun.
I started with some limits of recursive sequences, which actually are (a small) part of the class. Things like
and
which converges to the golden ratio. I resisted talking too much about the golden ratio and the Fibonacci sequence, because I figured many students had probably already seen it, or could easily learn about it online (which I suggested they do). Of course, at that point, you might as well write out, without any simplifying, the first couple of terms in that sequence and start talking about continued fractions, which I did.
Then I jumped to the (unsolved) 3n+1 problem: Consider the piecewise rule that defines $a_{n+1}$ to be $a_n/2$ if $a_n$ is even, and $3a_n+1$ if $a_n$ is odd. Now given any starting number $a_1$, the question is: does the sequence starting at $a_1$ and following the piecewise rule always eventually end up at the cycle 1, 4, 2, 1, 4, 2, 1...? I really love stating these simple problems (simple to state, that is) for my class, and pointing out that they are unsolved. I've also already mentioned the problem of finding odd perfect numbers.
From there, it's probably time to draw some pictures. The Koch snowflake is a fun example to do. I only talked about how it has an infinite perimeter, and will return later to finding the area, once we've done a little more with series.
Once you're on fractals, it's hard to resist the Mandelbrot set. This one's a little harder to talk about in a calc II class, because it involves complex numbers. But you can still talk about taking a function $f$ and a starting value $a_1$, and considering the sequence $a_1, f(a_1), f(f(a_1)), f(f(f(a_1))),\ldots $. This sequence is what you consider to determine if a point is in the Mandelbrot set, using the function $f(z)=z^2+a_1$ (a different function for each point you consider). So I showed a couple printed out pictures of the set, and encouraged my students to go online and look for more pictures.
I regret, just a little, missing the Cantor set in my discussion. Perhaps another day.
That's all I got to in class. Of course, there's still several weeks left in the semester, and lots of fun things that can be said with sequences and series. When we get to Taylor series, I'll probably tell them a little about my research, which is analogous to the series they'll be looking at. Since I'll be talking about my research, I'll also talk a bit about topology.
While I was wandering around wikipedia, looking for more fun things to talk about, I ran across the page on the ? function. I'd not heard of it before, but it looks pretty interesting. I should probably look at it some more sometime.
I started with some limits of recursive sequences, which actually are (a small) part of the class. Things like
$\sqrt{2}$, $\sqrt{2\sqrt{2}}$, $\sqrt{2\sqrt{2\sqrt{2}}}$, $\ldots\rightarrow 2$
and
$a_1=1, a_{n+1}=1+1/a_n$
which converges to the golden ratio. I resisted talking too much about the golden ratio and the Fibonacci sequence, because I figured many students had probably already seen it, or could easily learn about it online (which I suggested they do). Of course, at that point, you might as well write out, without any simplifying, the first couple of terms in that sequence and start talking about continued fractions, which I did.
Then I jumped to the (unsolved) 3n+1 problem: Consider the piecewise rule that defines $a_{n+1}$ to be $a_n/2$ if $a_n$ is even, and $3a_n+1$ if $a_n$ is odd. Now given any starting number $a_1$, the question is: does the sequence starting at $a_1$ and following the piecewise rule always eventually end up at the cycle 1, 4, 2, 1, 4, 2, 1...? I really love stating these simple problems (simple to state, that is) for my class, and pointing out that they are unsolved. I've also already mentioned the problem of finding odd perfect numbers.
From there, it's probably time to draw some pictures. The Koch snowflake is a fun example to do. I only talked about how it has an infinite perimeter, and will return later to finding the area, once we've done a little more with series.
Once you're on fractals, it's hard to resist the Mandelbrot set. This one's a little harder to talk about in a calc II class, because it involves complex numbers. But you can still talk about taking a function $f$ and a starting value $a_1$, and considering the sequence $a_1, f(a_1), f(f(a_1)), f(f(f(a_1))),\ldots $. This sequence is what you consider to determine if a point is in the Mandelbrot set, using the function $f(z)=z^2+a_1$ (a different function for each point you consider). So I showed a couple printed out pictures of the set, and encouraged my students to go online and look for more pictures.
I regret, just a little, missing the Cantor set in my discussion. Perhaps another day.
That's all I got to in class. Of course, there's still several weeks left in the semester, and lots of fun things that can be said with sequences and series. When we get to Taylor series, I'll probably tell them a little about my research, which is analogous to the series they'll be looking at. Since I'll be talking about my research, I'll also talk a bit about topology.
While I was wandering around wikipedia, looking for more fun things to talk about, I ran across the page on the ? function. I'd not heard of it before, but it looks pretty interesting. I should probably look at it some more sometime.
Wednesday, October 8, 2008
A Common Tangent
For what value of $a$ ($a>1$) does $a^x$ have a common tangent with its inverse, $\log_a x$?
Let $c$ be the $x$-coordinate of the point of tangency, so that the $y$-coordinate is $a^c$ and $\log_a c$. Setting these $y$-coordinates equal doesn't seem to get us anywhere.
So let's move to the tangent line. The derivative of $a^x$ is $a^x\cdot \ln a$, while the derivative of $\log_a x$ is $1/(x\cdot \ln a)$. Plugging in our common point, $x=c$, and setting the two slopes equal, we get $a^c\cdot \ln a=1/(c\cdot \ln a)$. Again, not obviously useful.
What gets me through this problem is thinking about it graphically. Since $a^x$ and $\log_a x$ are inverse functions, each is the mirror image of the other across the line $y=x$. This means that their common tangent line will, in fact, be that same line, $y=x$.
Therefore, the slope of the common tangent line will be 1. Our two ways to represent the slope are $a^c\cdot \ln a$ and $1/(c\cdot \ln a)$. Setting the second equal to 1 and solving for $c$, we get $c=1/(\ln a)$, which we could also write as $(\ln e)/(\ln a)=\log_a e$. The first way we represented the point of tangency was $(c,a^c)$, but since it is on the line $y=x$, this is also $(c,c)$, so $c=a^c$.
We're almost there. In $c=a^c$, replace the left-hand side with $1/(\ln a)$, from our slope calculations. On the right-hand side, replace $c$ with $\log_a e$. Then we get $1/(\ln a)=a^{\log_a e}=e$, so $1/e=\ln a$, and we see that $a=e^{(1/e)}$.
I'm not sure why I first asked this question. I was teaching calc 1 at the time, and probably looking for interesting homework problems. I seem to recall chickening out in assigning this as a problem. Perhaps some other semester. Either way, I thought it was cute.
Update 20081229: Apparently (according to the penguin dictionary of curious and interesting numbers) this value, $e^{(1/e)}$ is also the value of $x$ for which $x^{(1/x)}$ is a maximum. This isn't entirely correct, as the maximum occurs at $x=e$, and therefore $e^{(1/e)}$ is the maximum value. Wikipedia has a page.
Let $c$ be the $x$-coordinate of the point of tangency, so that the $y$-coordinate is $a^c$ and $\log_a c$. Setting these $y$-coordinates equal doesn't seem to get us anywhere.
So let's move to the tangent line. The derivative of $a^x$ is $a^x\cdot \ln a$, while the derivative of $\log_a x$ is $1/(x\cdot \ln a)$. Plugging in our common point, $x=c$, and setting the two slopes equal, we get $a^c\cdot \ln a=1/(c\cdot \ln a)$. Again, not obviously useful.
What gets me through this problem is thinking about it graphically. Since $a^x$ and $\log_a x$ are inverse functions, each is the mirror image of the other across the line $y=x$. This means that their common tangent line will, in fact, be that same line, $y=x$.
Therefore, the slope of the common tangent line will be 1. Our two ways to represent the slope are $a^c\cdot \ln a$ and $1/(c\cdot \ln a)$. Setting the second equal to 1 and solving for $c$, we get $c=1/(\ln a)$, which we could also write as $(\ln e)/(\ln a)=\log_a e$. The first way we represented the point of tangency was $(c,a^c)$, but since it is on the line $y=x$, this is also $(c,c)$, so $c=a^c$.
We're almost there. In $c=a^c$, replace the left-hand side with $1/(\ln a)$, from our slope calculations. On the right-hand side, replace $c$ with $\log_a e$. Then we get $1/(\ln a)=a^{\log_a e}=e$, so $1/e=\ln a$, and we see that $a=e^{(1/e)}$.
I'm not sure why I first asked this question. I was teaching calc 1 at the time, and probably looking for interesting homework problems. I seem to recall chickening out in assigning this as a problem. Perhaps some other semester. Either way, I thought it was cute.
Update 20081229: Apparently (according to the penguin dictionary of curious and interesting numbers) this value, $e^{(1/e)}$ is also the value of $x$ for which $x^{(1/x)}$ is a maximum. This isn't entirely correct, as the maximum occurs at $x=e$, and therefore $e^{(1/e)}$ is the maximum value. Wikipedia has a page.
Friday, October 3, 2008
Origami Numbers
Today I gave a (brief) talk for the Graduate Seminar in the math department here at UVA. This is an informal setting, which is only for grad students (no professors heckling the speaker). They're generally an hour, but I only went slightly over half of that time. All the same, it was a pretty comprehensible talk. At the very least, it was comprehensible material - who knows how the talk went.
The title for my talk was Origami Numbers. I walked through the first 5 of the Huzita-Hatori(-Justin-...) axioms [wikipedia], which are enough to do standard straight edge and compass constructions. The first 4 are pretty straight forward, and it's with the 5th that you start making interesting things - parabolas. Then with the 6th axiom, we are able to obtain cubic roots, showing that origami is more powerful than a straight edge and compass. A great reference, and my starting point, for all of this, is the book Project Origami by Thomas Hull (which has lots of other goodies).
One thing I found while preparing my talk was identified as Lill's method in this paper by Alperin and Lang. It's a graphical method for finding roots of polynomials, and I'd never seen it before. The paper 'Geometric Solutions of Algebraic Equations' by Riaz talks about it, as does this site, which I just found (so I should take another look at). Lill's method draws a piecewise linear path (starting, say, at O, and ending at T), where the lengths of pieces correspond to coefficients of your chosen polynomial. Then you are supposed to draw another path from O that bounces around off the lines you made and ends at T. This line shows you one of the roots for the original polynomial (see the above references for more details). It doesn't seem particularly practical if you want to find roots (I'd go for Newton's method, if all else failed), but it's fun to have a new graphical way to think about things.
The title for my talk was Origami Numbers. I walked through the first 5 of the Huzita-Hatori(-Justin-...) axioms [wikipedia], which are enough to do standard straight edge and compass constructions. The first 4 are pretty straight forward, and it's with the 5th that you start making interesting things - parabolas. Then with the 6th axiom, we are able to obtain cubic roots, showing that origami is more powerful than a straight edge and compass. A great reference, and my starting point, for all of this, is the book Project Origami by Thomas Hull (which has lots of other goodies).
One thing I found while preparing my talk was identified as Lill's method in this paper by Alperin and Lang. It's a graphical method for finding roots of polynomials, and I'd never seen it before. The paper 'Geometric Solutions of Algebraic Equations' by Riaz talks about it, as does this site, which I just found (so I should take another look at). Lill's method draws a piecewise linear path (starting, say, at O, and ending at T), where the lengths of pieces correspond to coefficients of your chosen polynomial. Then you are supposed to draw another path from O that bounces around off the lines you made and ends at T. This line shows you one of the roots for the original polynomial (see the above references for more details). It doesn't seem particularly practical if you want to find roots (I'd go for Newton's method, if all else failed), but it's fun to have a new graphical way to think about things.
Wednesday, October 1, 2008
Homework Helper
I've been a little bit frustrated with the way the discussion session for my calculus class has been going recently. That time is set aside as a time for students to ask whatever questions they have, without me lecturing on any new content. Of course, generally the questions they have are 'can you do this homework problem?' or 'I got stuck on this problem, can we go through it?'. Generally, those are fine questions that I'm happy to answer. However, I'm getting the impression that many of the students have not yet looked at the assignment yet, and are just waiting for me to do half of it for them. Of course, this'll come back to bite them on the exam, but it's fairly frustrating all around. So I've been trying to decide what to do about it.
It occurred to me today that even just answering those questions asked by the students who have looked at the assignment isn't very efficient. If they've already started, but gotten stuck, it'd be fairly quick for me to sit down with them individually, find their error, and send them on their merry way. Even there, though, that's not what I should be doing. It's easy for me to spot errors, generally. Especially when I've already looked at the problem with several other students. But it would be hugely valuable for students to be able to find their own mistakes. It can be maddening trying to find your own mistakes, of course, but it's an important skill to have.
A good way to practice finding mistakes, even if they get all of their own problems correct, would be to help identify mistakes in other people's work. Of course, this process can be ironed out a little online. I am envisioning a system where students can go and enter the work they have on a problem, up to the point where they got stuck. Then other students could go and try to find errors in people's work. This way people that get stuck can get help whenever it's convenient for them (as opposed to waiting for office hours or something), and students can practice finding errors in work.
It seems there should be some sort of credits system involved. At the beginning of the semester, students have, say... 3 credits, or 5 or something. A credit gives you permission to ask a question. To earn credits, you submit a bug report on another person's question. Perhaps a bug report just identifies what line the error occurs on, without identifying the error. And I guess answers would need to be verified before credit is added to the person who submitted the answer. Perhaps the person asking the question verifies it?
That's about as far as I've taken the idea today. Clearly there'd have to be an easy way to enter work, perhaps with some sort of graphical formula editor. Also probably some anonymity, so you can see questions, but not who submitted them (nor who answered them?). It also seems like what might happen is that the people who have the most questions might have a hard time spotting other people's mistakes in order to earn credits to ask more questions. So perhaps there's a way to account for that. Something like... if you earn lower than an N on the exam, each point less than that gets you a free credit?
Anyway, that's a day's thought on the idea. What do you all think? Do you know of a system that does something like this already? Could something like the above idea be worthwhile and helpful? How could it fail? Where does it need improvement? What additional policies might you use?
It occurred to me today that even just answering those questions asked by the students who have looked at the assignment isn't very efficient. If they've already started, but gotten stuck, it'd be fairly quick for me to sit down with them individually, find their error, and send them on their merry way. Even there, though, that's not what I should be doing. It's easy for me to spot errors, generally. Especially when I've already looked at the problem with several other students. But it would be hugely valuable for students to be able to find their own mistakes. It can be maddening trying to find your own mistakes, of course, but it's an important skill to have.
A good way to practice finding mistakes, even if they get all of their own problems correct, would be to help identify mistakes in other people's work. Of course, this process can be ironed out a little online. I am envisioning a system where students can go and enter the work they have on a problem, up to the point where they got stuck. Then other students could go and try to find errors in people's work. This way people that get stuck can get help whenever it's convenient for them (as opposed to waiting for office hours or something), and students can practice finding errors in work.
It seems there should be some sort of credits system involved. At the beginning of the semester, students have, say... 3 credits, or 5 or something. A credit gives you permission to ask a question. To earn credits, you submit a bug report on another person's question. Perhaps a bug report just identifies what line the error occurs on, without identifying the error. And I guess answers would need to be verified before credit is added to the person who submitted the answer. Perhaps the person asking the question verifies it?
That's about as far as I've taken the idea today. Clearly there'd have to be an easy way to enter work, perhaps with some sort of graphical formula editor. Also probably some anonymity, so you can see questions, but not who submitted them (nor who answered them?). It also seems like what might happen is that the people who have the most questions might have a hard time spotting other people's mistakes in order to earn credits to ask more questions. So perhaps there's a way to account for that. Something like... if you earn lower than an N on the exam, each point less than that gets you a free credit?
Anyway, that's a day's thought on the idea. What do you all think? Do you know of a system that does something like this already? Could something like the above idea be worthwhile and helpful? How could it fail? Where does it need improvement? What additional policies might you use?
Saturday, September 27, 2008
GEER
Today the annual Great Eastern Endurance Run was held at Sherando Lake. In fact, it is still being held. With the 6am start time, and a 19 hour time limit for the 100k group, there are likely plenty of runners still out there. I only ran the 50k, so I (thankfully) have been done for a little while.
I've been signed up for this run since sometime in the summer, and it has been my primary training goal since then. What is surprising, to me anyway, is that I don't think I ran too many runs in all that time that were longer than 20 miles. I think no more than 5. I have, though, run every single day for the last 6 weeks (as long as my 2 mile run yesterday counts). I'd like to continue this streak, and run a little tomorrow, but I'm going to see how I feel.
This last week I've been eating lots of pasta, and the last two days several bagels. Yesterday I drank a whole lot of water, and some Gatorade. Also in this past week I watched 'Running on the Sun', a documentary about the Badwater 135 mile ulta-marathon. I think it was a good move (and movie), since it made me much less nervous about my own run. My run seemed entirely reasonable next to those guys.
All the same, last night I was reasonably nervous. It didn't help that it had been raining for two days, and the forecast called for more today. I also wasn't looking forward to the waking up at 3:30 part of the plan. Luckily I got to bed pretty early, and my cats actually let me sleep. At some point a thunderstorm woke me up, so I got to worry about running in one of those. The primary concern there being that the GEER run is out in, and on top of, some of the mountains near the Blue Ridge Parkway. On top of a mountain doesn't sound like the ideal place to be in a thunderstorm.
Waking up early gave me time for a bagel and a banana, and some water. A little after 4 I met with another runner (doing the half marathon) that I was carpooling with, and then we picked up a volunteer for the run on our way out of town. Around 5 we were down at the park, still earlier than many people, which meant we got a good parking space, and getting our packets wasn't too much of a hastle. A couple of trips to the bathroom, a pre-race briefing, and it was go time.
Of course, it was still pretty dark out. Most of the runners had headlamps, and I was running just carrying a flashlight. The first mile or so was on the road, so it wasn't too much of a problem. The next stretch was up a pretty steep trail, but even so, the light wasn't too much of an issue. I was running, at the time, with the one other guy I knew, and we were somewhere in the top 10. Which was a good plan, so we didn't have to worry too much about getting stuck behind people on the relatively narrow trail. Eventually the sun starting coming out, and we were on top of a ridge, running in the fog or clouds or whatever. It was quite nice.
The rest stops all had lots of goodies. I went through handfuls of gummi bears, as well as a few oreos and pretzels, and even a quartered boiled potato. The stops also had bananas, but also other candies, mini chocolate bars, and even twinkies at one point. I had brought along some Clif Shot Blocks, courtesy of my carpooling friend, 3 packets of Gu, and a powerbar. The Shot Blocks and Gu were a huge help, and I never needed the powerbar.
By mile 14 I had moved up to somewhere around 5th place. The way the course is setup, there are two places where you run out and then turn around, and run back. This gives you a good chance to see how many people are ahead of you (if you are keeping track), and gives some indication how far back you are. I was surprised that the first place runner didn't seem much further ahead.
Around mile 20 I took 4th place, and within another 2 miles had passed two more runners on a bit of an uphill. I was quite surprised by all of this, but it made me pretty excited. Surely the top 3 finishers get something cool! Of course, that left me looking over my shoulder for the remaining several miles. Generally in the runs I do I start off far enough back that I spend the entire time passing people, which is a great feeling. Running in the front, all you can do is get passed. That's not as fun.
All the same, I decided I was going to hold on to second place. That (along with all the gummi bears and other goodies) kept me pushing the remaining miles away. My legs had started hurting a bit, and I was worried that my right quad was going to cramp up. It was not appreciating uphills, but luckily the last 7 or so miles are primarily downhill or flat.
I had decided not to run with a watch. This was my first run at this distance, I just wanted to go out and enjoy myself and not stress about my time. At some point about half way through I caught a guy looking at his watch, and got the time from him. I felt a little bad interrupting his run, but it seemed to work out ok. When I'd been thinking about the run, I had hoped to finish in 6 hours. With the weather, I thought 7 might be more reasonable. In the end, I came in just under 5 hours, holding on to second place (just about 4 minutes behind first). Which felt amazing. I'm still pretty excited about it. I got not only a pretty cool jacket (even though it's got a big logo on the back), but also an additional running t-shirt (all runners got 1 for the event).
It's been about 7 hours since I finished running. My legs can definitely tell that they did something this morning, but I feel pretty good. This week one of my professors was talking about how when he goes running he goes for short, hard runs. He wants to get tired as quickly as possible. I told him I'd much rather go and run for a few hours and get tired that way. Today I realized that perhaps part of that is that with a nice long run, you still feel like you did something hours, or even days later. Sure, a half hour hard run will make you tired, but it's not the same tired. Either way though, as long as you enjoy it, that's what counts. Right?
I've been signed up for this run since sometime in the summer, and it has been my primary training goal since then. What is surprising, to me anyway, is that I don't think I ran too many runs in all that time that were longer than 20 miles. I think no more than 5. I have, though, run every single day for the last 6 weeks (as long as my 2 mile run yesterday counts). I'd like to continue this streak, and run a little tomorrow, but I'm going to see how I feel.
This last week I've been eating lots of pasta, and the last two days several bagels. Yesterday I drank a whole lot of water, and some Gatorade. Also in this past week I watched 'Running on the Sun', a documentary about the Badwater 135 mile ulta-marathon. I think it was a good move (and movie), since it made me much less nervous about my own run. My run seemed entirely reasonable next to those guys.
All the same, last night I was reasonably nervous. It didn't help that it had been raining for two days, and the forecast called for more today. I also wasn't looking forward to the waking up at 3:30 part of the plan. Luckily I got to bed pretty early, and my cats actually let me sleep. At some point a thunderstorm woke me up, so I got to worry about running in one of those. The primary concern there being that the GEER run is out in, and on top of, some of the mountains near the Blue Ridge Parkway. On top of a mountain doesn't sound like the ideal place to be in a thunderstorm.
Waking up early gave me time for a bagel and a banana, and some water. A little after 4 I met with another runner (doing the half marathon) that I was carpooling with, and then we picked up a volunteer for the run on our way out of town. Around 5 we were down at the park, still earlier than many people, which meant we got a good parking space, and getting our packets wasn't too much of a hastle. A couple of trips to the bathroom, a pre-race briefing, and it was go time.
Of course, it was still pretty dark out. Most of the runners had headlamps, and I was running just carrying a flashlight. The first mile or so was on the road, so it wasn't too much of a problem. The next stretch was up a pretty steep trail, but even so, the light wasn't too much of an issue. I was running, at the time, with the one other guy I knew, and we were somewhere in the top 10. Which was a good plan, so we didn't have to worry too much about getting stuck behind people on the relatively narrow trail. Eventually the sun starting coming out, and we were on top of a ridge, running in the fog or clouds or whatever. It was quite nice.
The rest stops all had lots of goodies. I went through handfuls of gummi bears, as well as a few oreos and pretzels, and even a quartered boiled potato. The stops also had bananas, but also other candies, mini chocolate bars, and even twinkies at one point. I had brought along some Clif Shot Blocks, courtesy of my carpooling friend, 3 packets of Gu, and a powerbar. The Shot Blocks and Gu were a huge help, and I never needed the powerbar.
By mile 14 I had moved up to somewhere around 5th place. The way the course is setup, there are two places where you run out and then turn around, and run back. This gives you a good chance to see how many people are ahead of you (if you are keeping track), and gives some indication how far back you are. I was surprised that the first place runner didn't seem much further ahead.
Around mile 20 I took 4th place, and within another 2 miles had passed two more runners on a bit of an uphill. I was quite surprised by all of this, but it made me pretty excited. Surely the top 3 finishers get something cool! Of course, that left me looking over my shoulder for the remaining several miles. Generally in the runs I do I start off far enough back that I spend the entire time passing people, which is a great feeling. Running in the front, all you can do is get passed. That's not as fun.
All the same, I decided I was going to hold on to second place. That (along with all the gummi bears and other goodies) kept me pushing the remaining miles away. My legs had started hurting a bit, and I was worried that my right quad was going to cramp up. It was not appreciating uphills, but luckily the last 7 or so miles are primarily downhill or flat.
I had decided not to run with a watch. This was my first run at this distance, I just wanted to go out and enjoy myself and not stress about my time. At some point about half way through I caught a guy looking at his watch, and got the time from him. I felt a little bad interrupting his run, but it seemed to work out ok. When I'd been thinking about the run, I had hoped to finish in 6 hours. With the weather, I thought 7 might be more reasonable. In the end, I came in just under 5 hours, holding on to second place (just about 4 minutes behind first). Which felt amazing. I'm still pretty excited about it. I got not only a pretty cool jacket (even though it's got a big logo on the back), but also an additional running t-shirt (all runners got 1 for the event).
It's been about 7 hours since I finished running. My legs can definitely tell that they did something this morning, but I feel pretty good. This week one of my professors was talking about how when he goes running he goes for short, hard runs. He wants to get tired as quickly as possible. I told him I'd much rather go and run for a few hours and get tired that way. Today I realized that perhaps part of that is that with a nice long run, you still feel like you did something hours, or even days later. Sure, a half hour hard run will make you tired, but it's not the same tired. Either way though, as long as you enjoy it, that's what counts. Right?
Tuesday, September 23, 2008
Flatland, the Game
I was recently directed to the game here, and thought I'd forward it on to you, devoted reader. It's pretty entertaining, and a great way to think about dimensions. If you haven't read Flatland (wiki), you should probably get on that. After that, you can reward yourself by playing the game.
What happens in the game is two dimensional shapes (letters, numbers, etc) get sliced up into horizontal lines, and all you see is a movie of those horizontal lines. It is then your job to figure out what shape the came from. This is very much like the Sphere passing through the plane in Flatland.
Update 9/24: I was just reminded that Google recently did something where you can embed books. Flatland just happens to be one of them:
Hmm, I seem to not have it right. Suggestions anybody?
What happens in the game is two dimensional shapes (letters, numbers, etc) get sliced up into horizontal lines, and all you see is a movie of those horizontal lines. It is then your job to figure out what shape the came from. This is very much like the Sphere passing through the plane in Flatland.
Update 9/24: I was just reminded that Google recently did something where you can embed books. Flatland just happens to be one of them:
Hmm, I seem to not have it right. Suggestions anybody?
Saturday, September 20, 2008
News in Class
I was happy this week about the two new Mersenne primes being found/verified (mathworld). It gave me something outside or the usual calculus material to talk to my class about. Don't get me wrong, the calc is, of course, fascinating. But when you're in the midst of it, day in and day out, a change is welcome, I expect. I feel the same way about my research, incidentally. Looking at it on the broad scale, it's all interesting stuff. In the daily work, it's terribly frustrating. But I digress (seems to be what I do).
So to start class off Friday I mentioned the news. I asked if anybody had heard about it, and can't say I was particularly surprised that nobody had. I talked briefly about GIMPS and about the importance of primes in modern cryptography. I repeated the statements I'd seen in various blogs about the number of digits being vastly larger than the estimated number of atoms in the universe. The students seemed to be enjoying it, for which I was glad.
At some point, one of my students asked "What do you want to do when you grow up?" That may not be an exact quote, but that was the question. This still strikes me as fairly random for the conversation. I guess he was looking at the math I was talking about, perhaps wondering why anybody would care, and if that was the sort of thing I hoped to work on when I was done here. I had to answer honestly that I didn't quite know what I wanted to do, though I do enjoy teaching.
I'd like to continue bringing in math news items for my calc class. I feel fairly well connected online, so that if something I could share were to happen, I'd hear about it. But I'm trying to remember what the last similar sort of math news I could share would be, and it doesn't seem like the sort of thing that happens often. Anybody have any recommendations where I should be looking?
So to start class off Friday I mentioned the news. I asked if anybody had heard about it, and can't say I was particularly surprised that nobody had. I talked briefly about GIMPS and about the importance of primes in modern cryptography. I repeated the statements I'd seen in various blogs about the number of digits being vastly larger than the estimated number of atoms in the universe. The students seemed to be enjoying it, for which I was glad.
At some point, one of my students asked "What do you want to do when you grow up?" That may not be an exact quote, but that was the question. This still strikes me as fairly random for the conversation. I guess he was looking at the math I was talking about, perhaps wondering why anybody would care, and if that was the sort of thing I hoped to work on when I was done here. I had to answer honestly that I didn't quite know what I wanted to do, though I do enjoy teaching.
I'd like to continue bringing in math news items for my calc class. I feel fairly well connected online, so that if something I could share were to happen, I'd hear about it. But I'm trying to remember what the last similar sort of math news I could share would be, and it doesn't seem like the sort of thing that happens often. Anybody have any recommendations where I should be looking?
Saturday, September 6, 2008
Techniques of Integration
This semester I'm teaching Calc II from Stewart's text, Calculus. We start in chapter 7, which is about techniques of integration. One of my students made a very good observation early on in the process. We had already covered u-substitution and integration by parts, and were beginning trig integrals (integrating functions that are mostly build up from trig functions, products of sines and cosines and such). He realized that the 'technique' of the section was not, exactly, a new way to integrate. It was really just a way to re-write the integrand so that you could either apply u-substitution or parts. After pointing this out in class, I realized that he was correct, and that for our purposes, there really are only two techniques of integration - u-substitution and integration by parts. Everything past that is algebraic manipulations to change how the integrand 'looks'. That isn't to say the rest of it is easy. There are plenty of strange little tricks that pop up. Odd substitutions, or strange ways to split up the function.
I've made a point of trying to convince my class that they have to go home and do lots of integrals on their own. It won't matter how many examples I do in class (where the time is limited anyway, so we can't do too many). It is always easy to watch somebody doing math and think you understand, but then get completely stuck when you sit down to do similar problems yourself. Certainly there is value in doing examples in class. For example, trig substitutions are not something most people would be likely to come up with on their own. But after an example or two, the idea is something that can be readily used, and should be struggled with individually.
What I've been doing to present examples in class is to have the class guide me, as much as possible, through a problem. I put an integral up on the board and ask for ideas. We might go through a couple of failed u-substitutions or parts attempts before striking on the right way to proceed. But that's all part of the process, and it's good to see what happens when things don't work. After we get going, I try to get the students to tell me about each step. I hope that this keeps the class involved and focused on the problem. This means the examples take more time than if I was just presenting a quick path to the answer. So I'm, perhaps, not getting to as many examples as I could be, but I think I'm happy with how it's going so far.
We've still got partial fractions to go in the chapter. I think I'm happy with how the class is going so far, and hope that feeling continues.
I've made a point of trying to convince my class that they have to go home and do lots of integrals on their own. It won't matter how many examples I do in class (where the time is limited anyway, so we can't do too many). It is always easy to watch somebody doing math and think you understand, but then get completely stuck when you sit down to do similar problems yourself. Certainly there is value in doing examples in class. For example, trig substitutions are not something most people would be likely to come up with on their own. But after an example or two, the idea is something that can be readily used, and should be struggled with individually.
What I've been doing to present examples in class is to have the class guide me, as much as possible, through a problem. I put an integral up on the board and ask for ideas. We might go through a couple of failed u-substitutions or parts attempts before striking on the right way to proceed. But that's all part of the process, and it's good to see what happens when things don't work. After we get going, I try to get the students to tell me about each step. I hope that this keeps the class involved and focused on the problem. This means the examples take more time than if I was just presenting a quick path to the answer. So I'm, perhaps, not getting to as many examples as I could be, but I think I'm happy with how it's going so far.
We've still got partial fractions to go in the chapter. I think I'm happy with how the class is going so far, and hope that feeling continues.
Thursday, August 28, 2008
Back to School
The semester, here at UVA, started this week. In fact, I kicked it off with an 8am calculus class on the first day. It's been a busy week, largely due to my failure this summer to use my time wisely, but it's been fun.
Last semester I didn't teach. To compensate, I worked as a tutor for athletes in their tutoring center. It was ok, and certainly had it's moments, but it's nothing like having your own class that you meet with several times a week. I was nervous before the semester that I wouldn't have my old enthusiasm for teaching. It's always been what's gotten me through grad school (both the teaching now, and the hope to teach when I'm done). This summer, though, I was frustrated and couldn't motivate myself to think about the semester. It didn't seem like a good sign, but it's just a few days in, and I'm feeling better already.
I've been reminded of the fun of starting the fall semester, with mostly first year (we don't call them freshmen here, I don't know why) students in my class. This is my 5th year in grad school, and the first class of my own that I taught was 4 years ago. That means most of that class will be graduating this year (I hope). I believe that today, walking around on campus, I passed one of the students from that first semester, but they made no indication that they recognized me. That'll happen, I guess. They probably forgot most of the math even quicker.
I always want my class to go well (who doesn't?). I want to show them interesting things, and the things they'll need to know. Of course, in calc classes (any math classes), there is no shortage of interesting things. It's harder to figure out what it is they need to know. Since my class is one of several coordinated calculus classes, I at least have a pretty good idea what will be on exams. Certainly that's something they'll want to know. Whether it's the "right" content for the exam or not is harder to tell. Do we teach something because it's content a later class depends on? Or do we teach it just out of tradition? Is there a national standard base-level curriculum at the college level that we're trying to follow? Harder still is determining if there is a better way to structure a class than having it be largely exam (and homework set) based. Perhaps there's a nice way to do the class that's project based? And just how much technology should we be using? The old "calculators question".
The start of the semester has it's frustrations. We use the online homework system webwork in my class, and I really like it. Of course, every time I use it, I think about other ways to have it set up. Since it's open source, I should probably try to contribute some of these ideas in code. Not right now though. For now, I've got the usual issue of making sure everybody can log in. Some changes were made to our setup here, but there still seem to be some login issues. My class is also set up to use an online waitlist for enrollment. Which means I'm getting lots of emails from students asking to get in, and if they have a chance to get in off the waitlist. And since they've now missed two class periods... it's a hastle.
It'll be good when the administrivia settles down, and we can concentrate on the math. We're doing improper integrals tomorrow (and probably a little into Monday), and then spending several class periods covering the rest of the chapter on integration techniques. I've got an idea I'm excited about for teaching it, but I think I'll leave that for a later post, when I can tell you how it went. For now, the Mythbusters are busting some lunar landing myths.
Last semester I didn't teach. To compensate, I worked as a tutor for athletes in their tutoring center. It was ok, and certainly had it's moments, but it's nothing like having your own class that you meet with several times a week. I was nervous before the semester that I wouldn't have my old enthusiasm for teaching. It's always been what's gotten me through grad school (both the teaching now, and the hope to teach when I'm done). This summer, though, I was frustrated and couldn't motivate myself to think about the semester. It didn't seem like a good sign, but it's just a few days in, and I'm feeling better already.
I've been reminded of the fun of starting the fall semester, with mostly first year (we don't call them freshmen here, I don't know why) students in my class. This is my 5th year in grad school, and the first class of my own that I taught was 4 years ago. That means most of that class will be graduating this year (I hope). I believe that today, walking around on campus, I passed one of the students from that first semester, but they made no indication that they recognized me. That'll happen, I guess. They probably forgot most of the math even quicker.
I always want my class to go well (who doesn't?). I want to show them interesting things, and the things they'll need to know. Of course, in calc classes (any math classes), there is no shortage of interesting things. It's harder to figure out what it is they need to know. Since my class is one of several coordinated calculus classes, I at least have a pretty good idea what will be on exams. Certainly that's something they'll want to know. Whether it's the "right" content for the exam or not is harder to tell. Do we teach something because it's content a later class depends on? Or do we teach it just out of tradition? Is there a national standard base-level curriculum at the college level that we're trying to follow? Harder still is determining if there is a better way to structure a class than having it be largely exam (and homework set) based. Perhaps there's a nice way to do the class that's project based? And just how much technology should we be using? The old "calculators question".
The start of the semester has it's frustrations. We use the online homework system webwork in my class, and I really like it. Of course, every time I use it, I think about other ways to have it set up. Since it's open source, I should probably try to contribute some of these ideas in code. Not right now though. For now, I've got the usual issue of making sure everybody can log in. Some changes were made to our setup here, but there still seem to be some login issues. My class is also set up to use an online waitlist for enrollment. Which means I'm getting lots of emails from students asking to get in, and if they have a chance to get in off the waitlist. And since they've now missed two class periods... it's a hastle.
It'll be good when the administrivia settles down, and we can concentrate on the math. We're doing improper integrals tomorrow (and probably a little into Monday), and then spending several class periods covering the rest of the chapter on integration techniques. I've got an idea I'm excited about for teaching it, but I think I'll leave that for a later post, when I can tell you how it went. For now, the Mythbusters are busting some lunar landing myths.
Saturday, August 16, 2008
TN Roadtrip, Day 2 (13 Aug, 2008)
I had thought about getting a pretty early start to the morning to go for a run at an area of the park known as Cades Cove. There is a scenic 11 mile road there, with lots of places to stop and look at things, like historic log cabins. All of the roads in the park (that I was on) had lots of places to stop and look at the scenery, and probably all of the stops are worthwhile, if you've got lots of time. Anyway, the reason I had thought about doing this run was that the road is closed Wednesday (which it was) and Saturday mornings until 10am, to allow cyclists and pedestrians to have the road to themselves. However, when I talked to somebody at the information desk the day before, he mentioned that I was very likely to see bear if I did this. Seeing bear driving is one thing, but running is a whole new matter. Especially because one of the first things they tell you, for if you encounter a bear, is not to run. Besides his warning, at dinner the night before I had seen on the news that there had been a bear attack on a human that same day. It was the first attack since 2000, and billed as quite rare, but I was still a bit un-nerved. I also saw in the news that there was a local school that wasn't starting on time because they couldn't get their budget worked out. I was pretty surprised by this, but when I mentioned it to a friend, he said this was happening in several places. He said some of the schools are going to 4-day weeks to save some costs.
So I decided not to go on the run, planning instead on hiking a trail loop starting at Cades Cove. Cades Cove is less than 30 miles from the Sugarlands Visitor's Center, at the entrance to the park, and it takes about an hour to drive. I figured I could head out and do the hike, then drive the popular road loop. One of the first things I did when I started the hike was to pick up a walking stick. The main reason was that I didn't want to have to be finding sticks to defend myself with from a bear as it attacked me. I wanted to have one ready to go, just in case. Probably silly, but there you have it.
Perhaps a mile or so in on the trail, I came to a clearing with this log cabin:
 While still basically in sight of the cabin, along the trail, I saw 2 dear in the woods. I was glad I was doing the hike, instead of one of the many people on the road who didn't get to see the deer. Sure, a cabin or two is probably interesting to see, but deer are more fun. They didn't seem too upset with me, and let me pass without running away. The trail continued slightly uphill for a short while, at which point I encountered my first bear of the day. It was right there on the trail, and actually I kinda came around a corner and saw it, so got closer than I was happy with. After backing off, and getting my picture,
While still basically in sight of the cabin, along the trail, I saw 2 dear in the woods. I was glad I was doing the hike, instead of one of the many people on the road who didn't get to see the deer. Sure, a cabin or two is probably interesting to see, but deer are more fun. They didn't seem too upset with me, and let me pass without running away. The trail continued slightly uphill for a short while, at which point I encountered my first bear of the day. It was right there on the trail, and actually I kinda came around a corner and saw it, so got closer than I was happy with. After backing off, and getting my picture,
 I waited around and listened to the bear wander off slowly into the woods. When it sounded far enough away, I continued on along the trail.
I waited around and listened to the bear wander off slowly into the woods. When it sounded far enough away, I continued on along the trail.
From that point on, I was pretty nervous hiking. Every sound in the woods gave me pause. Not long (15 minutes, maybe) after my first bear encounter, I was heading up a larger hill, and heard something off to my left. I couldn't see anything, but it wasn't far off the trail. So I backed up, and tried making a little bit of noise (coughing, tossing a stone at a larger rock on the trail). I wasn't trying to scare whatever it was, I just wanted it to know I was there, so I didn't surprise it. Bear Grylls [wiki] taught me to make my presence known. Seems to me a frightened animal is more dangerous, and I didn't want to encounter any of that. So anyway, I stood there for a while, not seeing anything, and not hearing it wander off. So I tried heading up the trail again, keeping a keen eye out. Before I got too close, I saw that it was, indeed, another bear. They tell you, in addition to not running, that if a bear attacks you are supposed to make yourself look bigger, by holding up your arms and standing on a rock or tree stump. Being downhill, this knowledge made me fairly uncomfortable. I backed off again from the bear (couldn't get a good picture this time), and decided that perhaps I'd try my luck along another trail (one that I was actually more interested in, since it was in higher mountains).
On my way back down the trail, right where I had seen the first bear, I heard something that sounded large on the side of the trail again. This time the sound was coming up, toward the trail, from a little valley, so I couldn't see anything. I started moving faster, keeping myself pointed toward the noise, holding my arms up, and talking at the noise. I never did see anything, happily. Shortly thereafter, I passed a few hikers heading back in that direction, and told them to keep an eye out. They seemed eager to see a bear, so I hope they got the opportunity. I, on the other hand, was fed up with seeing bears, and was glad not to have any more encounters. However, the rest of the day I was nervous, and on high alert.
The next main portion of my trip was a long hike along the Bull Head and Rainbow Falls trails (in that order), and was probably the highlight of my Smoky Mountains touring. This is a 12+ mile loop, and there's an additional half-mile spur you can do near the top to bring you to some lodges near the peak of Mt. Le Conte, bringing the total to 13+ miles. This made me feel a little better about not running in the morning, since I'd still be getting a workout. The hike took me just more than 5 hours, but I was kinda pushing myself. The first 2 hours were nearly all uphill, which I simply loved (modulo the being nervous about bears bit). I saw only 4 other hikers this entire time, in 2 groups of 2. It's wonderful how much elevation you can get walking uphill for 2 hours. I was also amazed by how much the vegetation changed along my walk. The trip back down Rainbow Falls trail bring you past, get this - Rainbow Falls. Amazing huh? The falls themselves weren't entirely impressive, though I expect that at wetter times of the year this might not be the case. Even so, it's a beautiful area.
 The falls are about 2.5 miles from the nearby parking area, so this section of trail is a little bit busier. One group I caught up to mentioned a mama bear with cubs that I'd apparently just missed on my way down the trail. The bears were apparently just on the other side of the creek from the trail. Probably the cubs were cute, but mama bears are especially dangerous, so I'm not sure how disappointed I am that I missed these guys.
The falls are about 2.5 miles from the nearby parking area, so this section of trail is a little bit busier. One group I caught up to mentioned a mama bear with cubs that I'd apparently just missed on my way down the trail. The bears were apparently just on the other side of the creek from the trail. Probably the cubs were cute, but mama bears are especially dangerous, so I'm not sure how disappointed I am that I missed these guys.
After the hike, I followed the Roaring Fork Motor Nature Trail, which is a single-lane, one-way road. I think if you buy the \$1 visitor's guide, it has some information that accompanies the various numbered signs you'll see along the way. It was a quite nice loop, and fun to drive, with lots of nice scenery.
 This picture was taken from a stop about a mile from the start of the loop. I almost wished I'd just stayed there the remaining time until sunset. I bet it was amazing. I'd recommend this loop to anybody who was in the area. It doesn't take too long to drive (I think it's only about 6 miles), and is quite pretty.
This picture was taken from a stop about a mile from the start of the loop. I almost wished I'd just stayed there the remaining time until sunset. I bet it was amazing. I'd recommend this loop to anybody who was in the area. It doesn't take too long to drive (I think it's only about 6 miles), and is quite pretty.
So there you have it. The Smoky Mountains Park is wonderful, and I highly recommend it. Stop in the visitor's center on your way in and buy some maps to both support the park and help you decide what to do with your time. If you plan on hiking alone, some pepper spray might also help you feel more comfortable about bear encounters. I found the webpage also to be helpful, with lots of good information about planning your trip. The trails I was on were all well marked, and very well maintained. There were signs at all the trail junctions indicating which trail was which, and also indicating distances to the next trail. If you are driving the park, pick any (better: several) of the little stop-offs to get out of your car and wander around. I've posted a few more of my (favorite) pictures over on flickr, if you are interested.
So I decided not to go on the run, planning instead on hiking a trail loop starting at Cades Cove. Cades Cove is less than 30 miles from the Sugarlands Visitor's Center, at the entrance to the park, and it takes about an hour to drive. I figured I could head out and do the hike, then drive the popular road loop. One of the first things I did when I started the hike was to pick up a walking stick. The main reason was that I didn't want to have to be finding sticks to defend myself with from a bear as it attacked me. I wanted to have one ready to go, just in case. Probably silly, but there you have it.
Perhaps a mile or so in on the trail, I came to a clearing with this log cabin:
 While still basically in sight of the cabin, along the trail, I saw 2 dear in the woods. I was glad I was doing the hike, instead of one of the many people on the road who didn't get to see the deer. Sure, a cabin or two is probably interesting to see, but deer are more fun. They didn't seem too upset with me, and let me pass without running away. The trail continued slightly uphill for a short while, at which point I encountered my first bear of the day. It was right there on the trail, and actually I kinda came around a corner and saw it, so got closer than I was happy with. After backing off, and getting my picture,
While still basically in sight of the cabin, along the trail, I saw 2 dear in the woods. I was glad I was doing the hike, instead of one of the many people on the road who didn't get to see the deer. Sure, a cabin or two is probably interesting to see, but deer are more fun. They didn't seem too upset with me, and let me pass without running away. The trail continued slightly uphill for a short while, at which point I encountered my first bear of the day. It was right there on the trail, and actually I kinda came around a corner and saw it, so got closer than I was happy with. After backing off, and getting my picture, I waited around and listened to the bear wander off slowly into the woods. When it sounded far enough away, I continued on along the trail.
I waited around and listened to the bear wander off slowly into the woods. When it sounded far enough away, I continued on along the trail.From that point on, I was pretty nervous hiking. Every sound in the woods gave me pause. Not long (15 minutes, maybe) after my first bear encounter, I was heading up a larger hill, and heard something off to my left. I couldn't see anything, but it wasn't far off the trail. So I backed up, and tried making a little bit of noise (coughing, tossing a stone at a larger rock on the trail). I wasn't trying to scare whatever it was, I just wanted it to know I was there, so I didn't surprise it. Bear Grylls [wiki] taught me to make my presence known. Seems to me a frightened animal is more dangerous, and I didn't want to encounter any of that. So anyway, I stood there for a while, not seeing anything, and not hearing it wander off. So I tried heading up the trail again, keeping a keen eye out. Before I got too close, I saw that it was, indeed, another bear. They tell you, in addition to not running, that if a bear attacks you are supposed to make yourself look bigger, by holding up your arms and standing on a rock or tree stump. Being downhill, this knowledge made me fairly uncomfortable. I backed off again from the bear (couldn't get a good picture this time), and decided that perhaps I'd try my luck along another trail (one that I was actually more interested in, since it was in higher mountains).
On my way back down the trail, right where I had seen the first bear, I heard something that sounded large on the side of the trail again. This time the sound was coming up, toward the trail, from a little valley, so I couldn't see anything. I started moving faster, keeping myself pointed toward the noise, holding my arms up, and talking at the noise. I never did see anything, happily. Shortly thereafter, I passed a few hikers heading back in that direction, and told them to keep an eye out. They seemed eager to see a bear, so I hope they got the opportunity. I, on the other hand, was fed up with seeing bears, and was glad not to have any more encounters. However, the rest of the day I was nervous, and on high alert.
The next main portion of my trip was a long hike along the Bull Head and Rainbow Falls trails (in that order), and was probably the highlight of my Smoky Mountains touring. This is a 12+ mile loop, and there's an additional half-mile spur you can do near the top to bring you to some lodges near the peak of Mt. Le Conte, bringing the total to 13+ miles. This made me feel a little better about not running in the morning, since I'd still be getting a workout. The hike took me just more than 5 hours, but I was kinda pushing myself. The first 2 hours were nearly all uphill, which I simply loved (modulo the being nervous about bears bit). I saw only 4 other hikers this entire time, in 2 groups of 2. It's wonderful how much elevation you can get walking uphill for 2 hours. I was also amazed by how much the vegetation changed along my walk. The trip back down Rainbow Falls trail bring you past, get this - Rainbow Falls. Amazing huh? The falls themselves weren't entirely impressive, though I expect that at wetter times of the year this might not be the case. Even so, it's a beautiful area.
 The falls are about 2.5 miles from the nearby parking area, so this section of trail is a little bit busier. One group I caught up to mentioned a mama bear with cubs that I'd apparently just missed on my way down the trail. The bears were apparently just on the other side of the creek from the trail. Probably the cubs were cute, but mama bears are especially dangerous, so I'm not sure how disappointed I am that I missed these guys.
The falls are about 2.5 miles from the nearby parking area, so this section of trail is a little bit busier. One group I caught up to mentioned a mama bear with cubs that I'd apparently just missed on my way down the trail. The bears were apparently just on the other side of the creek from the trail. Probably the cubs were cute, but mama bears are especially dangerous, so I'm not sure how disappointed I am that I missed these guys.After the hike, I followed the Roaring Fork Motor Nature Trail, which is a single-lane, one-way road. I think if you buy the \$1 visitor's guide, it has some information that accompanies the various numbered signs you'll see along the way. It was a quite nice loop, and fun to drive, with lots of nice scenery.
 This picture was taken from a stop about a mile from the start of the loop. I almost wished I'd just stayed there the remaining time until sunset. I bet it was amazing. I'd recommend this loop to anybody who was in the area. It doesn't take too long to drive (I think it's only about 6 miles), and is quite pretty.
This picture was taken from a stop about a mile from the start of the loop. I almost wished I'd just stayed there the remaining time until sunset. I bet it was amazing. I'd recommend this loop to anybody who was in the area. It doesn't take too long to drive (I think it's only about 6 miles), and is quite pretty.So there you have it. The Smoky Mountains Park is wonderful, and I highly recommend it. Stop in the visitor's center on your way in and buy some maps to both support the park and help you decide what to do with your time. If you plan on hiking alone, some pepper spray might also help you feel more comfortable about bear encounters. I found the webpage also to be helpful, with lots of good information about planning your trip. The trails I was on were all well marked, and very well maintained. There were signs at all the trail junctions indicating which trail was which, and also indicating distances to the next trail. If you are driving the park, pick any (better: several) of the little stop-offs to get out of your car and wander around. I've posted a few more of my (favorite) pictures over on flickr, if you are interested.
Friday, August 15, 2008
TN Roadtrip, Day 1 (12 Aug, 2008)
I came into the Great Smoky Mountains National Park from the North, coming in off route 40 headed towards Knoxville, TN. After getting off 40, I drove through Sevierville (where my hotel was) and Pidgeon Forge, and just bypassed Gatlinburg which is on the edge of the park. I was shocked by how much Sevierville/Pidgeon Forge (there isn't much of a gap between them) put me off. Along the main stretch of road, there are an incredible number of hotels, chain restaurants, flashing lights and neon signs. There were many 'Dinner and a Show' places, raceways and go carting, a little bungee jump place, indoor skydiving (wind tunnel), arcades, a 'Movie Rider', skate park, 'Jurassic Jungle Boat Ride', and probably many more strange things. I have no idea what the area is built up like this. Dollywood is nearby, I don't know if that's what started it or not. I expected to be vaguely in the middle of nowhere when I got near the park, but instead felt like I was at a circus or something. Only two of the attraction sorts of things were things I wasn't sad to see. The first was cheap helicopter rides. I don't know what it gets you, but all the places had signs that said \$10. The second was pancake houses. There are a half dozen 'Flapjacks' alone (it's 20 miles or so from route 40 to the park - the traffic lights have mile marker indications, which I liked), and many others going by other names. I did eat at a Flapjacks, but wasn't entirely impressed, least of all by their pancakes. I also ate at a 'Buddy's BBQ', which I was pleased to find.
Anyway, I got to the park, and stopped at the Sugarlands Visitors Center, which is basically the first thing you run into when you get to the park. The park doesn't charge admission, so there were lots of donation boxes around. Some of them were associated with buying maps, and I ended up getting a 'Starter Pack' with many maps and guides for only \$5. Seemed like the best deal. Also at the visitor's center (and various other parking areas) there was a First Amendment Expression Area, which I was humored by.

From the visitor's center I headed down Newfound Gap Road on my way to Clingman's Dome. This is at the highest peak in the park, and therefore 'On Top of Old Smoky'. The road to Clingman's Dome ends at a parking lot, and then it's a paved walkway the remaining half mile to the top of the mountain. It's a somewhat steep walkway, and pretty busy.
 But that's to be expected, being the highest peak. At the top is an observation deck, with a looping ramp up.
But that's to be expected, being the highest peak. At the top is an observation deck, with a looping ramp up.
 I wasn't expecting that, but it puts you above the trees so you can see all the way out.
I wasn't expecting that, but it puts you above the trees so you can see all the way out.
Once I was back in my car, driving back down from the dome, I saw my first bear of the trip. It was right along the side of the road, happily just poking it's nose around in the grass, presumably eating something. It seemed not to care at all about the cars and spectators it was attracting. After a few minutes, I wanted to keep moving, so I drove by it, and snapped a picture out my window:

Now mid-afternoon, I headed to my hotel for check-in. The main thing that kicked off this road trip was a Nine Inch Nails concert in Knoxville, which was this evening. On my way in, I'd seen signs that there was some construction on the roads in Knoxville right where I wanted to be, so I wanted to get in early, in case I needed to find my way around. It turned out to not be any problem at all, so I had plenty of time to try to find somewhere to eat. I didn't find much near the convention center, where the concert was, besides 'Market Square' which had a few places, only one of which (that I noticed) was a national chain place (a Subway). I ate at Trio's, which I'd happily go back to.
The concert was, of course, awesome. NIN always put on quite a show. If they release a dvd for this tour (as they have for 2 previous tours), I'll be delighted to get it. They do lots of fun video things, and had an awesome setup. Best of all, they played for nearly 2 hours. With a music library stretching back 20 years, they had no problem filling the time, and drew from all of their albums. The opening act was a band called 'Deerhunter', who, apparently, were from Pidgeon Forge. When the tour was announced, a little 'sampler' was released (still available, at that link), with a song from each of the various opening bands that would be joining NIN along the way. Sadly, Deerhunter was perhaps my least favorite of the three. At the concert, their music was decent enough, but they didn't put on much of a show. The lead singer (a guy) came out dressed as a cheerleader, skirt and all, and couldn't have weighed more than... his guitar probably. It was incredible, and kinda disturbing. They didn't seem to get much respect or adoration from the crowd. All the same, I had a great time. I've not been to many concerts, and the experience in the mosh pit was something few for me. I've now been crowd-surfed over, which is an indication that I was pretty close to the front, I reckon.
Anyway, I got to the park, and stopped at the Sugarlands Visitors Center, which is basically the first thing you run into when you get to the park. The park doesn't charge admission, so there were lots of donation boxes around. Some of them were associated with buying maps, and I ended up getting a 'Starter Pack' with many maps and guides for only \$5. Seemed like the best deal. Also at the visitor's center (and various other parking areas) there was a First Amendment Expression Area, which I was humored by.

From the visitor's center I headed down Newfound Gap Road on my way to Clingman's Dome. This is at the highest peak in the park, and therefore 'On Top of Old Smoky'. The road to Clingman's Dome ends at a parking lot, and then it's a paved walkway the remaining half mile to the top of the mountain. It's a somewhat steep walkway, and pretty busy.
 But that's to be expected, being the highest peak. At the top is an observation deck, with a looping ramp up.
But that's to be expected, being the highest peak. At the top is an observation deck, with a looping ramp up. I wasn't expecting that, but it puts you above the trees so you can see all the way out.
I wasn't expecting that, but it puts you above the trees so you can see all the way out.Once I was back in my car, driving back down from the dome, I saw my first bear of the trip. It was right along the side of the road, happily just poking it's nose around in the grass, presumably eating something. It seemed not to care at all about the cars and spectators it was attracting. After a few minutes, I wanted to keep moving, so I drove by it, and snapped a picture out my window:

Now mid-afternoon, I headed to my hotel for check-in. The main thing that kicked off this road trip was a Nine Inch Nails concert in Knoxville, which was this evening. On my way in, I'd seen signs that there was some construction on the roads in Knoxville right where I wanted to be, so I wanted to get in early, in case I needed to find my way around. It turned out to not be any problem at all, so I had plenty of time to try to find somewhere to eat. I didn't find much near the convention center, where the concert was, besides 'Market Square' which had a few places, only one of which (that I noticed) was a national chain place (a Subway). I ate at Trio's, which I'd happily go back to.
The concert was, of course, awesome. NIN always put on quite a show. If they release a dvd for this tour (as they have for 2 previous tours), I'll be delighted to get it. They do lots of fun video things, and had an awesome setup. Best of all, they played for nearly 2 hours. With a music library stretching back 20 years, they had no problem filling the time, and drew from all of their albums. The opening act was a band called 'Deerhunter', who, apparently, were from Pidgeon Forge. When the tour was announced, a little 'sampler' was released (still available, at that link), with a song from each of the various opening bands that would be joining NIN along the way. Sadly, Deerhunter was perhaps my least favorite of the three. At the concert, their music was decent enough, but they didn't put on much of a show. The lead singer (a guy) came out dressed as a cheerleader, skirt and all, and couldn't have weighed more than... his guitar probably. It was incredible, and kinda disturbing. They didn't seem to get much respect or adoration from the crowd. All the same, I had a great time. I've not been to many concerts, and the experience in the mosh pit was something few for me. I've now been crowd-surfed over, which is an indication that I was pretty close to the front, I reckon.
Subscribe to:
Posts (Atom)