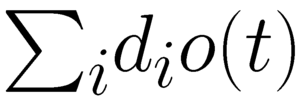I never have any idea what to do with students who are going through some sort of difficulty outside of the classroom. I understand that bad things happen all of the time, and there's never a good time for it. But at the same time, I don't see how it helps for a student to tell me what they are going through, even just in broad terms. They don't have to tell me if there is some family issue, or relationships, or health, or... anything. There are outside circumstances, I understand, and that's all I really need to know about.
But I don't know how to actually interact with these students when they come to my office and want to tell me what is going on. Most of me wants to stop them from talking about what, in any general or specific terms, is going on. There's nothing I can do about it. But I don't want to come across as not caring. Of course I'm sorry that they are going through whatever difficulty it is.
Sunday, July 19, 2009
Wednesday, July 1, 2009
Summer Calc II, Second Half
My summer calculus class is almost over. Not that I don't love teaching, or calculus, or that I don't like my students, but I won't mind when it's over. I've got plenty of other things I should be (and shouldn't be :)) working on this summer. But anyway. Our final exam is tomorrow.
Hopefully it will go better than the first midterm. Admittedly, the first midterm was after only 8 class periods, and had content from 4 different chapters. The exam I wrote is one I was pretty pleased with. Other instructors told me that it was conceptual, which I take as a complement. The average, though, was sadly low. Our final, tomorrow, only covers series. I don't think it's quite as interesting as the first, but other instructors seem to think it is still fair. So we'll see.
I approached series a little bit differently than I have in the past. The last few semesters, I've followed the outline of the book, starting with sequences, then series, on to convergence tests, power series, and wrapping up with Taylor series. I thought this semester I'd try to motivate the discussion of series a little differently. Instead of just "I'd really like to add up a bunch of numbers", I began with Taylor polynomials because "I'd really like to approximate a function". This felt like a good fit with the earlier material, when we found arc lengths (and similar things) by approximating the calculation with an easy one and taking a limit (and calling it an integral). So we're going to approximate a function by an "easy" one (polynomial) and then take a limit.
After that goal is set, it's easy enough to say that "good approximation" means "the derivatives match" (at the point in question), and derive the formula for the coefficients of the Taylor polynomial. Then I pointed out that we could do the process as long as we want and make polynomials of degrees as large as we wanted, and pointed out that this would end up looking very much like taking a limit.
Next I talked about power series in general, power series being what we get "in the limit" of our Taylor polynomial calculations. I talked about differentiating, integrating, and substituting into power series, to try to give some indication that they are useful and easy to work with. I'm not sure this part went over particularly well. It might have been better to do this later, with radius and interval of convergence (see below).
So once we have power series, I pointed out that evaluating a power series at a point meant you had to sum infinitely many values. But that we basically knew how, since we started with Taylor polynomials and took the limit. To sum infinitely many values, you just take a limit of partial sums. So I talked a little about general sequences and series at this point (and also spend an hour talking about fun examples - continued fractions, 3n+1 problem, koch snowflake, cantor set,...).
Then we had a whole day (2 hours of class, +/-) where I just talked about all of the convergence tests, followed by a day for them to work on convergence tests in class (work on homework, or just try other problems). I think that for a summer class, with the odd schedules and times, this almost works. During a normal semester, though, I wouldn't do things this way. I'd probably try to get the students to learn the problems from the book themselves. In fact, I did try this last semester, but that's a separate story.
My philosophy with the convergence tests (and most other topics) is that there isn't much point in my doing more than one or two examples at the board. Math is always easier when you watch somebody else do it. The only way to get comfortable with the convergence tests is to work a whole bunch of problems for yourself. Hopefully the longer-than-average assignment I gave my class helped them gain that comfort.
Once we have convergence tests, we can return to power series, and ask "for which x is this power series defined?" I like to think that this helped tie things together from our initial discussion of power series. I'm not convinced that's the case, but I'm also not sure how to tell (ask the students?). I think this maybe would be a better time for the discussion about how to manipulate power series than early on. I'll probably try it this way next time (this fall, for my fourth straight calc II class).
That covers all of the content for the series chapter. So then I spent a full class period talking about all sorts of fun and exciting uses of series. Today in class I gave them time to review (gave them a copy of last semester's exam, essentially), after answering whatever review questions they came in with.
I'm hoping this exam goes well. And that after it's all over, I have a productive summer.
Hopefully it will go better than the first midterm. Admittedly, the first midterm was after only 8 class periods, and had content from 4 different chapters. The exam I wrote is one I was pretty pleased with. Other instructors told me that it was conceptual, which I take as a complement. The average, though, was sadly low. Our final, tomorrow, only covers series. I don't think it's quite as interesting as the first, but other instructors seem to think it is still fair. So we'll see.
I approached series a little bit differently than I have in the past. The last few semesters, I've followed the outline of the book, starting with sequences, then series, on to convergence tests, power series, and wrapping up with Taylor series. I thought this semester I'd try to motivate the discussion of series a little differently. Instead of just "I'd really like to add up a bunch of numbers", I began with Taylor polynomials because "I'd really like to approximate a function". This felt like a good fit with the earlier material, when we found arc lengths (and similar things) by approximating the calculation with an easy one and taking a limit (and calling it an integral). So we're going to approximate a function by an "easy" one (polynomial) and then take a limit.
After that goal is set, it's easy enough to say that "good approximation" means "the derivatives match" (at the point in question), and derive the formula for the coefficients of the Taylor polynomial. Then I pointed out that we could do the process as long as we want and make polynomials of degrees as large as we wanted, and pointed out that this would end up looking very much like taking a limit.
Next I talked about power series in general, power series being what we get "in the limit" of our Taylor polynomial calculations. I talked about differentiating, integrating, and substituting into power series, to try to give some indication that they are useful and easy to work with. I'm not sure this part went over particularly well. It might have been better to do this later, with radius and interval of convergence (see below).
So once we have power series, I pointed out that evaluating a power series at a point meant you had to sum infinitely many values. But that we basically knew how, since we started with Taylor polynomials and took the limit. To sum infinitely many values, you just take a limit of partial sums. So I talked a little about general sequences and series at this point (and also spend an hour talking about fun examples - continued fractions, 3n+1 problem, koch snowflake, cantor set,...).
Then we had a whole day (2 hours of class, +/-) where I just talked about all of the convergence tests, followed by a day for them to work on convergence tests in class (work on homework, or just try other problems). I think that for a summer class, with the odd schedules and times, this almost works. During a normal semester, though, I wouldn't do things this way. I'd probably try to get the students to learn the problems from the book themselves. In fact, I did try this last semester, but that's a separate story.
My philosophy with the convergence tests (and most other topics) is that there isn't much point in my doing more than one or two examples at the board. Math is always easier when you watch somebody else do it. The only way to get comfortable with the convergence tests is to work a whole bunch of problems for yourself. Hopefully the longer-than-average assignment I gave my class helped them gain that comfort.
Once we have convergence tests, we can return to power series, and ask "for which x is this power series defined?" I like to think that this helped tie things together from our initial discussion of power series. I'm not convinced that's the case, but I'm also not sure how to tell (ask the students?). I think this maybe would be a better time for the discussion about how to manipulate power series than early on. I'll probably try it this way next time (this fall, for my fourth straight calc II class).
That covers all of the content for the series chapter. So then I spent a full class period talking about all sorts of fun and exciting uses of series. Today in class I gave them time to review (gave them a copy of last semester's exam, essentially), after answering whatever review questions they came in with.
I'm hoping this exam goes well. And that after it's all over, I have a productive summer.
Subscribe to:
Posts (Atom)