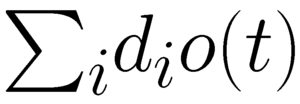Since I tried a few silly things with my class this semester, I wrote a couple of extra questions on the end-of-the-semester evaluations to get student feedback on them. In particular, I set up homework so that students were to choose which problems to do on an individual basis, and I orchestrated a class project to write our own textbook. Overall, student feedback was not as negative as I had anticipated, which was nice. Of course, only 19 of 39 students completed the evaluation...
Homework feedback was the least negative of the two. Of the 19 responses, 11 said they liked it. Others seemed to think it was ok, but didn't provide enough structure (not unexpectedly). A handful thought it would have been better if they were given some direction of things to focus on (I still don't see, for our class, how there was that much to choose from). One student apparently initially thought they would like the setup, but ended up not. A few flat-out didn't like it. Alas. I still like the basic idea.
The project was a source of frustration for all involved, which is too bad.
I'll begin with some of their feedback. A few students noted that they liked the idea of the project (and the project itself), working together to make something other students might use. And a few said they learned some things (mostly whichever mini project they were on), even if it wasn't related to the course content as listed on the syllabus. Some students found it tedious, and busy work, and would have rathered just do more homework problems (this confuses me, because assigning problems seems like busy work to me). A couple think in-class time to work with groups would have been good, which I can definitely see. And one student's comment, about wanting to see all the work at the end, makes me think another part could be added to the assignment, in which students would present their mini project work at the end of the semester - I think this would be valuable (even if the work is all accessible on the wiki anyway).
And now, my perspective. First off, there was no point in letting this project exist for half of the semester, as almost all of the work seemed to get done on due dates, right up to the minute. Apparently about two weeks probably could have produced the same result.
One of the parts I thought would be best was the "write questions" and then "write answers to classmates questions" parts. This seemed straight-forward enough to me, and the mostly clearly useful for our course content. Questions were due in two blocks, on a couple of Friday evenings. I'd then spend the evening (my life is that exciting!) formatting things so it all looked somewhat uniform, and randomly assigning problems to students. Due dates were such that after a block of questions were written, the answers were due two weeks later. I wanted to have a quick turn-around time from problems being written to problems being assigned, so students could have more time working on well-written answers, as well as working out issues with the questions (poor wording, ambiguity, problems in the wrong sections, etc). Of course, by my previous comment, I really could have spared more time before assigning answers. And I should have, using the time to edit the questions for clarity and content, since apparently students writing answers mostly didn't feel the need to do so (despite it being written as part of the assignment). I'm also concerned that I should have tried harder to see if questions (and, later, answers) were copied from the textbook, early on in the process. And for some reason I expected all of my students to follow the guidelines about how many of which questions (difficulty/content) to write (and write them on time), so that I when I redistributed them, everybody would end up writing the same number of answers. Silly me.
Clearly that part of the project would need to be tweaked (completely dismantled and reassembled) for future use.
The other useful part of the project was the MiniProjects, which students were put into groups for, based on initial project proposals they submitted. This part of the project was intended to involve group meetings about 2-3 weeks before the semester ended so students could show me rough drafts (ideally just little issues remaining). It became clear, the week of these meetings, that only very few of the groups had done anything at all (those that had done things had done well), which was hugely frustrating. Several students came to the meetings hoping I'd tell them what do to do get started, with no ideas of their own. This was weeks after their project proposals and group assignments. Perhaps a few more meetings would have been a good idea.
Anyway, eventually a whole-book pdf was compiled by one of the groups, of all of the sections and pages of questions and answers, and lots of appendices containing the further research found as part of many of the MiniProjects. It comes out to 126 pages, of which I wrote about 35-40. I'd share the book with you, but students at UVA own the intellectual property to their work, and I clearly can't force them to give me their work so I can just post it online for free for anybody, nor would I try. However, I did tell them I'd release all of my base effort under a CC license, and told students that if they wanted to contribute their work similarly, I'd be happy to compile it. I've got signatures from 18 students that I can gather their work up into a bundle, which I fully intend to do in the coming weeks. I'm sure you'll hear more about it, if you're still reading this far into this post.
Monday, December 20, 2010
Sunday, December 12, 2010
Textbook Poll Results
Here are results from the first 77 responses to the textbook poll I mentioned recently. Charts are via Google's api, and numbers for the pie charts are percentages. I don't really know who ended up taking this, unfortunately, but my guess is that it is predominantly undergraduates at the University of Virginia.
- How likely would you be to purchase an optional textbook for a math course, if it were a reasonable price?
One of the fill-ins was: "Only if I perceived to be beneficial to my grade."
- Would you be comfortable using a student compiled textbook for a math course if your professor used it as the main textbook for the course?
- If you were taking a mathematics course and your professor provided you access to a free, online textbook in addition to your regular textbook, how likely would you be to reference the additional book for extra help and problems?
With a write-in "Depends on how well I understand the respective material."
- If a free digital copy of a textbook were legally available online, how likely would you be to buy a paper version?
- To what extent do you use your textbook in a math course? (multiple answers allowed, counts are number of respondents). The available answers were: "I real all relevant sections", "I skim example problems", "To do extra unassigned problems", "I focus on highlighted formulas", and "Only to do assigned problems".
Also a few fill-ins:
- Whenever I find I don't understand a topic I find the book explains it in a very simple understandable way.
- To try and find lost-related Equations
- Reference tables and equations in the back of book
- never
- Paperweight
- I do not own a textbook
- What changes/improvements would you like to see in how textbooks are structured?
Here's a sampling of answers:
- A couple comments about digital versions:
- "Putting textbooks online is hard for a lot of people (including myself!) to read from"
- "would prefer more kindle/e-reader-friendly books".
- Some about textbook usage in relation to class:
- "Perhaps if the textbook order followed the order are curriculum is taught."
- "Force students to use the textbook by alternating between online homework and maybe do quizzes based out of the book."
- "More similarity between the material taught in class and the material in the textbook and more sample problems."
- Some miscellaneous comments:
- "Less space on corny math jokes. More space on actual math."
- "More colorful; Black and white only is hard to look at and discourages you from using the book"
- Most of the responses were about examples and solutions:
- More examples
- More and more-detailed examples of problems; detailed answers in the back of the book
- More concrete examples and better solutions to the problems
- To have more examples problems where the problem is worked out step by step and explained
- clearer example problem presentation, clearer explanation of concepts
- In the example section of a chapter, I would like to see questions that are actually challenging, something that will actually be on the test. The textbook companies always provide the most basic examples, which most of the time, are not helpful for actual application later.
- When working out sample problems in each section split the problem into two sides. The left side would have the actual mathematical processes with each individual step shown. The right side would have the processes explained in words, not just symbols, which would make each step more understandable.
- more steps to the answers
- i would like to see example problems with full explanations of EACH step as well as a break down of definitions into simpler terms.
- Solutions that show the work
- More examples of how to solve hard problems, instead of just the basics. If the point is to learn the material, why just assign really difficult applications of the principles as problems when you could just as easily show us how to solve them in the body of the text?
- Many of the problems in the textbook seem rather easy compared to the problems on WebWork or questions asked on the test. It would be nice to have more problems in the textbook that would be comparable in difficulty to the UVA level of calculus.
- Answers to every problem not just odds.
- I think they are good but textbooks ought to have answers for all the problems - our textbook has answers for just the odd problems.
- More examples would be nice, because for many people that is the best way to learn - by examining problems and understanding why they are done a particular way. Also, better explanations of each step in given examples.
- Make more sense with it. Show answers for EVERY PROBLEM and show how the answer is SOLVED. Don't just use one example and then hope that the people can figure out how to do the rest of the assigned problems. Show all the steps involved to do each problem. Make an ""answer"" textbook instead of putting the answers in the back, so that way people can have the assigned problems AND the answer textbook open so they can understand the steps required to solve the problems. It may sound like people are just going to copy the work, and maybe they will, but the answers will show a thorough way of how to solve the problems, which will help people do much better on quizzes and tests overall.
- A couple comments about digital versions:
- Do you have any additional comments or feedback?
A sampling:
- "The text book we have no has not helped me at all - my teacher explains everything we need to know, so the only use it has is practice problems. In the future I would suggest saving students thousands of dollars and not making a textbook mandatory"
- "Try not to use all the example problems from the text book, it takes away a student's resource if the lectures are not helping."
- "I haven't opened my textbook at all this year."
- There were also two comments about how textbooks are too expensive.
There was also a fairly lengthy response expounding on the virtues of e-books and the ePub format in particular. It mentioned how videos right in the textbook "could be a cool new way of learning mathematics." And apparently this student loves his or her iPad:
iPad and tablets will run rampant in education/academia in the next 5 years. My iPad has transformed the way I take notes, do my reading for class, organize my life, and access my material. I have never been so prepared for class in my life, I don't necessarily do anything beyond what is assigned, I just now have the time to do it on-the-go, interactively, and efficiently. It's one of those cases where I am working smarter, not harder. And I owe it all to the iPad streamlining my academic life. Textbooks are going paperless and nearly half of mine are (all on my iPad).
Monday, November 29, 2010
NCR Trail Marathon
This past Saturday I ran the NCR Trail Marathon. I'd definitely recommend it for anybody looking for a marathon in the Baltimore area in November. It's a primarily flat course (besides the first and last mileish) on some sort of paved path (but probably more forgiving than roads), and pretty, with lots of trees and water and farms. It'd probably be even nicer when there are leaves on the trees, but still. It's basically an out-and-back, for whatever that's worth. Before I get to talking about my run (sorry), I want to thank all of the volunteers, staff, supporters, etc. You all were fantastic, and deserve medals for standing out there in the cold all that time. The aid station volunteers were great about calling out where water was, versus gatorade. And all of the cheering was wonderful; I definitely got a good boost every time. Thanks, all.
My goal going in was to qualify for Boston, requiring a 3:10:59 clock time. I wasn't really sure I could do it, though I was pretty confident I could get a 3:20. I tried not to get my hopes up too much, but couldn't really help it. I've been feeling like I've been running pretty well recently, even if I've only averaged 33 mile weeks for the past 9, topping out with one 41 mile week. My longest training run was a 2:34 21.2 miles, 3 weeks ago.
I got up in the 5 o'clock hour, dawdled for about an hour, slowly getting ready, and stressing myself out. My sister, like a champ, got up early to head out to the course with me, and we got to the Sparks Elementary School, where the start/finish are, by about 8. It's a 9am start time, which is sorta nice and late. Of course, that meant another hour of sitting around, stressing myself out. And checking out all the other runners. Oh man, that guy looks serious. Are there supposed to be holes in that guy's shirt in those places? And look at all those ultra shirts. And Boston apparel. Etc.
I started off a few rows back, worried that the trail might not be too wide, and I'd get cut off (no worries there, it's a car's width throughout). Put in a sub-6:50 first mile, and joked with the guy next to me... "just a few more of those, huh?" It was sort of fun looking at the runners around me... that guy surely is gonna blow up... I wonder if I can keep up with that guy for a few minutes. Etc.
At the first water stop I threw water at my face. Some of it made it to my mouth. The rest reminded me that it was probably not yet 40 degrees, and windy. Somehow the wind honestly managed to be against us in both directions. I'm not the only one who says so, so it must be true.
By mile 2 or 3, the pack had thinned out pretty well, and I was basically running with another guy (who I recognized from the shuttle, also trying to qualify for Boston), putting in just-faster-than-7s. Before too long he got a little lead, and I was worried about blowing up, myself, so I let him go. About the same time another guy caught up to me, and we also ran together for several miles, still putting in 7s pretty consistently. At every mile marker we'd both check our watches. I'd do a quick calculation in my head to make sure we were still on track, and he'd check a pace chart on his arm. After the first one or two, I said something about "nice pace, huh?" and he didn't respond. Headphones. Alright, fine. We must have run about 7 or 8 miles together in silence, putting in basically 7 minute miles throughout. Occasionally I'd think he was getting ahead, and I'd think, "ok, just let him go, you gotta do your own thing." And then I'd think, "see what he's got, maybe you two can push each other the whole time". And, "should he be breathing that hard if he's hoping to keep this pace for 2 more hours? Am I breathing that hard?" Somewhere along the line he dropped off behind me. So I ran on alone.
Since the course is basically an out-and-back, you see lots of mile markers, in addition to the ones that are just part of the NCR trail. I definitely got in to looking for the backs of the second-half signs, then the yellow NCR signs, and then the first-half signs (and the other order after the turn around). At some point there's a "fitness walk" along the side of the trail. 10ish stations set up with "do so-and-so exercise here". I was a little amused.
Hit the half in the 1:31 minute, a pace just over 7:00s. Then the turn around. And over the second half, somehow managed to basically keep my pace, and pass several runners. According to the results, 8 of the 10 guys who came in just after me overall were ahead of me at the half. So that was sorta nice. I'd keep seeing people ahead and think, ok, you'll just tail this guy in. And then I'd catch up. And nobody passed me. It was kinda crazy.
Somewhere around mile 18 I started hurting. I was hoping that'd hold off until 20, but there it was. Just kept telling myself I only had so much time left. And wondering if I'd hit my 3:10. I knew I was doing ok with all of the 7s I'd put in, so thought about trying to drop off to 7:15s or 7:30s consistently. But I couldn't convince myself I knew what that pace felt like, so I just kept pushing. I couldn't tell what I was running, so it was always a pleasant surprise when another mile would drop off at somewhere in the 7s.
At mile 22 I was ahead of my 21 mile training run time, feeling pretty rough, but basically optimistic. With every mile I kept saying, "ok, you could run 9s and still make 3:10", and then it was 10s... Of course, each mile the calculations got more difficult, with my mind not really sure why we were still doing this. What time was I at at the last mile? What mile am I at? Am I still running 7s, or am I at 12s? (I know that my 23rd mile was still sub-7, which still surprises me) Why is that girl running toward me smiling? (It was my sister, who had headed out for a run of her own) Is it a bad sign that my hands hurt like that?
With about a mile to go I scooped up one more runner. And saw two ahead of me. I figured they'd keep their lead, but it kept getting shorter. Coming up the final hill, a little before the final turn, the three of us were together. I feel sorta bad passing people at the end like that, but I gave it a kick to see if I had anything left (gotta do my run, not anybody else's, after all), and if they'd answer. I sorta did, and they sorta didn't. Came in at 3:04:55 clock time, 20th overall, and 5th in my age division (2 ahead of me were in the top 5 overall, so I could have picked up my 3rd place award for my group). Pretty proud of myself, if the length of this post didn't give that away. Sorry.
The folks at the end grabbed my tear-off bib number, grabbed my chip, and gave me a metal blanket and medal. I took a few more steps and plopped down in a chair. Other runners walked on by, "good run". I rarely had energy to answer. It was still cold and windy out, so I walked a little bit further down the hill, trying to make it back in to the school, but had to sit down again. My legs hurt, and with the blanket, I could just about avoid the wind. At some point while I was sitting there, my sister made it back from her run, and sat with me. She must have been cold, but she stayed with me anyway. A few more small walks and stops, and I eventually made it back into the school (cursing the whole way). Stopped right inside the doorway huddled up against a wall. One lady walked by and saw me shivering and gave me her metal blanket. I kept shivering. My sister kept chuckling. People kept walking by telling me about the hot soup just inside. Eventually I made it back onto my feet, and to the soup table. I must have looked pretty ragged; the lady seemed a bit concerned. I was shaking quite a bit, so she gave me some coffee to warm me up, and some soup. Made it to a seat at a table, and didn't get up for probably half an hour. Sat there with my sister, talking about our runs, shivering. Feeling like the other runners didn't look nearly as rough as I felt. The soup really was quite good. And my sister was awesome.
I think it was probably about 45 minutes after I stopped running that I finally stopped shivering. Sorta makes me think probably I gave just about all I could to the run, which is a good feeling. I definitely don't think I could have done any better. And now I guess I start looking forward to Boston :) Of course, there's an ultra in March I've got my eyes on...
My goal going in was to qualify for Boston, requiring a 3:10:59 clock time. I wasn't really sure I could do it, though I was pretty confident I could get a 3:20. I tried not to get my hopes up too much, but couldn't really help it. I've been feeling like I've been running pretty well recently, even if I've only averaged 33 mile weeks for the past 9, topping out with one 41 mile week. My longest training run was a 2:34 21.2 miles, 3 weeks ago.
I got up in the 5 o'clock hour, dawdled for about an hour, slowly getting ready, and stressing myself out. My sister, like a champ, got up early to head out to the course with me, and we got to the Sparks Elementary School, where the start/finish are, by about 8. It's a 9am start time, which is sorta nice and late. Of course, that meant another hour of sitting around, stressing myself out. And checking out all the other runners. Oh man, that guy looks serious. Are there supposed to be holes in that guy's shirt in those places? And look at all those ultra shirts. And Boston apparel. Etc.
I started off a few rows back, worried that the trail might not be too wide, and I'd get cut off (no worries there, it's a car's width throughout). Put in a sub-6:50 first mile, and joked with the guy next to me... "just a few more of those, huh?" It was sort of fun looking at the runners around me... that guy surely is gonna blow up... I wonder if I can keep up with that guy for a few minutes. Etc.
At the first water stop I threw water at my face. Some of it made it to my mouth. The rest reminded me that it was probably not yet 40 degrees, and windy. Somehow the wind honestly managed to be against us in both directions. I'm not the only one who says so, so it must be true.
By mile 2 or 3, the pack had thinned out pretty well, and I was basically running with another guy (who I recognized from the shuttle, also trying to qualify for Boston), putting in just-faster-than-7s. Before too long he got a little lead, and I was worried about blowing up, myself, so I let him go. About the same time another guy caught up to me, and we also ran together for several miles, still putting in 7s pretty consistently. At every mile marker we'd both check our watches. I'd do a quick calculation in my head to make sure we were still on track, and he'd check a pace chart on his arm. After the first one or two, I said something about "nice pace, huh?" and he didn't respond. Headphones. Alright, fine. We must have run about 7 or 8 miles together in silence, putting in basically 7 minute miles throughout. Occasionally I'd think he was getting ahead, and I'd think, "ok, just let him go, you gotta do your own thing." And then I'd think, "see what he's got, maybe you two can push each other the whole time". And, "should he be breathing that hard if he's hoping to keep this pace for 2 more hours? Am I breathing that hard?" Somewhere along the line he dropped off behind me. So I ran on alone.
Since the course is basically an out-and-back, you see lots of mile markers, in addition to the ones that are just part of the NCR trail. I definitely got in to looking for the backs of the second-half signs, then the yellow NCR signs, and then the first-half signs (and the other order after the turn around). At some point there's a "fitness walk" along the side of the trail. 10ish stations set up with "do so-and-so exercise here". I was a little amused.
Hit the half in the 1:31 minute, a pace just over 7:00s. Then the turn around. And over the second half, somehow managed to basically keep my pace, and pass several runners. According to the results, 8 of the 10 guys who came in just after me overall were ahead of me at the half. So that was sorta nice. I'd keep seeing people ahead and think, ok, you'll just tail this guy in. And then I'd catch up. And nobody passed me. It was kinda crazy.
Somewhere around mile 18 I started hurting. I was hoping that'd hold off until 20, but there it was. Just kept telling myself I only had so much time left. And wondering if I'd hit my 3:10. I knew I was doing ok with all of the 7s I'd put in, so thought about trying to drop off to 7:15s or 7:30s consistently. But I couldn't convince myself I knew what that pace felt like, so I just kept pushing. I couldn't tell what I was running, so it was always a pleasant surprise when another mile would drop off at somewhere in the 7s.
At mile 22 I was ahead of my 21 mile training run time, feeling pretty rough, but basically optimistic. With every mile I kept saying, "ok, you could run 9s and still make 3:10", and then it was 10s... Of course, each mile the calculations got more difficult, with my mind not really sure why we were still doing this. What time was I at at the last mile? What mile am I at? Am I still running 7s, or am I at 12s? (I know that my 23rd mile was still sub-7, which still surprises me) Why is that girl running toward me smiling? (It was my sister, who had headed out for a run of her own) Is it a bad sign that my hands hurt like that?
With about a mile to go I scooped up one more runner. And saw two ahead of me. I figured they'd keep their lead, but it kept getting shorter. Coming up the final hill, a little before the final turn, the three of us were together. I feel sorta bad passing people at the end like that, but I gave it a kick to see if I had anything left (gotta do my run, not anybody else's, after all), and if they'd answer. I sorta did, and they sorta didn't. Came in at 3:04:55 clock time, 20th overall, and 5th in my age division (2 ahead of me were in the top 5 overall, so I could have picked up my 3rd place award for my group). Pretty proud of myself, if the length of this post didn't give that away. Sorry.
The folks at the end grabbed my tear-off bib number, grabbed my chip, and gave me a metal blanket and medal. I took a few more steps and plopped down in a chair. Other runners walked on by, "good run". I rarely had energy to answer. It was still cold and windy out, so I walked a little bit further down the hill, trying to make it back in to the school, but had to sit down again. My legs hurt, and with the blanket, I could just about avoid the wind. At some point while I was sitting there, my sister made it back from her run, and sat with me. She must have been cold, but she stayed with me anyway. A few more small walks and stops, and I eventually made it back into the school (cursing the whole way). Stopped right inside the doorway huddled up against a wall. One lady walked by and saw me shivering and gave me her metal blanket. I kept shivering. My sister kept chuckling. People kept walking by telling me about the hot soup just inside. Eventually I made it back onto my feet, and to the soup table. I must have looked pretty ragged; the lady seemed a bit concerned. I was shaking quite a bit, so she gave me some coffee to warm me up, and some soup. Made it to a seat at a table, and didn't get up for probably half an hour. Sat there with my sister, talking about our runs, shivering. Feeling like the other runners didn't look nearly as rough as I felt. The soup really was quite good. And my sister was awesome.
I think it was probably about 45 minutes after I stopped running that I finally stopped shivering. Sorta makes me think probably I gave just about all I could to the run, which is a good feeling. I definitely don't think I could have done any better. And now I guess I start looking forward to Boston :) Of course, there's an ultra in March I've got my eyes on...
Sunday, November 28, 2010
A Textbook Poll
In association with my class project of making our own book, one of my students has made a quick poll about textbooks. If you are a student, or wouldn't mind sharing this with any you know, we'll be happy to have your feedback. So, if you've got a minute,
Sunday, November 21, 2010
Well, In My Defense...
I gave my Ph.D. thesis defense the other day. It's sort of an odd thing to call it a defense, for a math paper. You argue in the humanities (I think, I haven't spent much time there). In math, you're just presenting facts, it's (sorta) the nice thing about math. Well, that's the ideal, I guess. There were certainly some weak joints in my work, but, as expected, people didn't have enough time to really stress about them. Which is nice.
When the thesis committee told me they were allowed to torture me with questions after everybody left, I told them, "knock yourselves out." Got a little chuckle. One professor asked what the hardest part was. I had wondered if somebody would. The hardest part was convincing myself it was worth doing --- was more worth doing than the other things I wanted to be doing. Luckily, he extended his question a little before I got to it (besides a grin), and I ended up just telling him about what math took the longest to piece together. The same professor asked if I was going to do anything with this later, that it would require some re-writing. I told him I had no intent of doing much with it, but that it would be freely available online, and he could do with it as he liked. He also said they could send me some changes that I should make. I guess when I said "whatever flips your switch", he realized I didn't care much to do them, and he, appropriately, didn't care enough to send the suggested changes to me. I didn't make any comments about how they were still allowed to make me jump through hoops, which is a little too bad.
The talk itself was fun. I do enjoy giving math talks, especially when I understand what I'm talking about. Threw in a couple jokes, got a few chuckles, put at least one professor to sleep. All in a day. I've got some notes about the presentation itself on my other blog. Or you can poke around the thesis material at my homepage.
So that means I'm nearly done. Still some administrative nonsense to do. And still a few weeks of "teaching". But nearly there.
When the thesis committee told me they were allowed to torture me with questions after everybody left, I told them, "knock yourselves out." Got a little chuckle. One professor asked what the hardest part was. I had wondered if somebody would. The hardest part was convincing myself it was worth doing --- was more worth doing than the other things I wanted to be doing. Luckily, he extended his question a little before I got to it (besides a grin), and I ended up just telling him about what math took the longest to piece together. The same professor asked if I was going to do anything with this later, that it would require some re-writing. I told him I had no intent of doing much with it, but that it would be freely available online, and he could do with it as he liked. He also said they could send me some changes that I should make. I guess when I said "whatever flips your switch", he realized I didn't care much to do them, and he, appropriately, didn't care enough to send the suggested changes to me. I didn't make any comments about how they were still allowed to make me jump through hoops, which is a little too bad.
The talk itself was fun. I do enjoy giving math talks, especially when I understand what I'm talking about. Threw in a couple jokes, got a few chuckles, put at least one professor to sleep. All in a day. I've got some notes about the presentation itself on my other blog. Or you can poke around the thesis material at my homepage.
So that means I'm nearly done. Still some administrative nonsense to do. And still a few weeks of "teaching". But nearly there.
Sunday, November 14, 2010
A Homework Experiment
At the beginning of the semester I decided to try something new with homework. Basically, students were supposed to do as many problems as they thought necessary to get the understanding of the material that they desired. If a student notices that there are essentially one or two types of problems in a section (as is frequently the case with our textbook), they probably don't need to do many problems. Other students might require more practice to feel comfortable with material. I gave them the responsibility of deciding for themselves how much to do.
Each week, students turned in a sheet saying which problems they did, how they would grade their own understanding, what major and minor issues they had, any questions they had, and a "well-written" solution to one problem. Grading has been pretty easy, and I've basically just graded on completion. It's been nice to get questions on homework (and respond with individual answers), and to see students evaluating their own mistakes. Quality of "well-written" solutions varied a bit, but I did see many good ones.
Our first exam really didn't go so great, even though I hadn't seen many students rate their own understanding on homeworks much below a B. I think this was partially due to this relaxed structure of homework. After the exam I asked the students to tell me (anonymous feedback was fine) if they wanted to see anything change to make the class better for them, and I never heard anything. Our second exam, last week, went a bit better, and I like to think perhaps study habits had improved.
Anyway, part of what I wanted to see, doing homework this way, was if there was a relationship between number of problems done for homework and exam scores. I've been keeping track of how many problems each student did each week (probably miscounting slightly occasionally), and so after this last exam I broke out gnumeric. In the name of privacy (thanks to those in my twitter/facebook network for their thoughts here), I varied each point by some random small perturbation, and have removed axes labels and scales, with the following result:
The x-axis is number of problems done, and the y-axis is the sum of the two exam grades divided by the sum of the two best possible exam grades. It's nice to see that the linear fit has a positive slope, at least. The correlation coefficient for the actual scores was about 0.23, so not so great. What I find slightly interesting is that it just about looks like (and does in the actual scores too) there are 3 clusters... a large collection on the left, another 8 there in the middle, and 3 more at the end who did lots of problems.
I know it wasn't particularly scientific, or rigorous, but that's what I've got. I never told the students I was collecting this data (I'll show this to them in class tomorrow), in hopes that they wouldn't be just making up how much they did, but it's still a possibility. I almost wish I'd kept track of the scores students gave themselves, but it's too late now.
Speaking of class tomorrow, I better go sort out what we're doing...
Each week, students turned in a sheet saying which problems they did, how they would grade their own understanding, what major and minor issues they had, any questions they had, and a "well-written" solution to one problem. Grading has been pretty easy, and I've basically just graded on completion. It's been nice to get questions on homework (and respond with individual answers), and to see students evaluating their own mistakes. Quality of "well-written" solutions varied a bit, but I did see many good ones.
Our first exam really didn't go so great, even though I hadn't seen many students rate their own understanding on homeworks much below a B. I think this was partially due to this relaxed structure of homework. After the exam I asked the students to tell me (anonymous feedback was fine) if they wanted to see anything change to make the class better for them, and I never heard anything. Our second exam, last week, went a bit better, and I like to think perhaps study habits had improved.
Anyway, part of what I wanted to see, doing homework this way, was if there was a relationship between number of problems done for homework and exam scores. I've been keeping track of how many problems each student did each week (probably miscounting slightly occasionally), and so after this last exam I broke out gnumeric. In the name of privacy (thanks to those in my twitter/facebook network for their thoughts here), I varied each point by some random small perturbation, and have removed axes labels and scales, with the following result:
The x-axis is number of problems done, and the y-axis is the sum of the two exam grades divided by the sum of the two best possible exam grades. It's nice to see that the linear fit has a positive slope, at least. The correlation coefficient for the actual scores was about 0.23, so not so great. What I find slightly interesting is that it just about looks like (and does in the actual scores too) there are 3 clusters... a large collection on the left, another 8 there in the middle, and 3 more at the end who did lots of problems.
I know it wasn't particularly scientific, or rigorous, but that's what I've got. I never told the students I was collecting this data (I'll show this to them in class tomorrow), in hopes that they wouldn't be just making up how much they did, but it's still a possibility. I almost wish I'd kept track of the scores students gave themselves, but it's too late now.
Speaking of class tomorrow, I better go sort out what we're doing...
Monday, September 27, 2010
Class Project
We're making a textbook. Or at least we're going to try.
On Friday I told my class I wanted to do a class project, where we all work together making a textbook. I told them I thought it would be fun and interesting and worthwhile. I told them that in addition to writing problems and solutions, like a textbook should have, they would also get to do something fun, of their own choosing, to make it a good project. I told them they had the weekend to think about it, and that we'd talk about it in class today. Attendance was unexpectedly low today, but the impression I got was that the majority of those in attendance were for the project. So we're going to try it.
The course I'm teaching is "Financial Math", and the textbook that has been used for this class in previous semesters, as decided by somebody else in the department some time in the past, is The Mathematics of Interest Rates and Finance, by Guthrie and Lemon (covering, approximately, chapters 1-6). I'm not a huge fan of this book, and I don't really hide that from my students. Rumor was that the department was considering finding a different book for this semester. I don't know how hard they looked, but we're using this book again. I'm pretty sure it's not because this is the best book we could be using. But what do I know. Anyway, the point is, this book is the basis for the course, and so will be the inspiration, if you will, for the book my class puts together.
I've been typing up my notes as I go, so I've got an outline and first draft of content for the first few chapters, so far. I told my students I'd write the first draft of the remaining content as well. There will be 3 parts of the project, from the perspective of it being a graded assignment. First, students will be put into groups and required to edit a few sections. I'm not much of a writer (in case you hadn't noticed), and I've done basically no editing of what I've written, so that'll be an important task. Next up, they will have to write some problems, and then I'll have them also write solutions for somebody else's problems. Finally, the fun part. They're to come up with a "mini project" that they want to do to make the book better. I've suggested things like:
On Friday I told my class I wanted to do a class project, where we all work together making a textbook. I told them I thought it would be fun and interesting and worthwhile. I told them that in addition to writing problems and solutions, like a textbook should have, they would also get to do something fun, of their own choosing, to make it a good project. I told them they had the weekend to think about it, and that we'd talk about it in class today. Attendance was unexpectedly low today, but the impression I got was that the majority of those in attendance were for the project. So we're going to try it.
The course I'm teaching is "Financial Math", and the textbook that has been used for this class in previous semesters, as decided by somebody else in the department some time in the past, is The Mathematics of Interest Rates and Finance, by Guthrie and Lemon (covering, approximately, chapters 1-6). I'm not a huge fan of this book, and I don't really hide that from my students. Rumor was that the department was considering finding a different book for this semester. I don't know how hard they looked, but we're using this book again. I'm pretty sure it's not because this is the best book we could be using. But what do I know. Anyway, the point is, this book is the basis for the course, and so will be the inspiration, if you will, for the book my class puts together.
I've been typing up my notes as I go, so I've got an outline and first draft of content for the first few chapters, so far. I told my students I'd write the first draft of the remaining content as well. There will be 3 parts of the project, from the perspective of it being a graded assignment. First, students will be put into groups and required to edit a few sections. I'm not much of a writer (in case you hadn't noticed), and I've done basically no editing of what I've written, so that'll be an important task. Next up, they will have to write some problems, and then I'll have them also write solutions for somebody else's problems. Finally, the fun part. They're to come up with a "mini project" that they want to do to make the book better. I've suggested things like:
- making diagrams, charts, graphics to accompany the text
- writing sections on using calculators, or spreadsheets
- writing historical or real-world content
- convert everything to other digital formats
But I'm hoping they come up with more. Things they actually want to do. I'm curious to see what they come up with. I told them to dream big, and don't worry if it was too big (we can trim it to something manageable for the purposes of grading). It'll be good to have ideas bouncing around.
The overall organization of this is still coming together. There's a bit of work that seems to need to happen on my end to get things off the ground. Next week we've got a midterm, and then we've got a little fall break, so hopefully by the time we return, in just over 2 weeks, things will be all organized for the class.
I've been LaTeXing my notes, but it seems like using the wiki feature of our course management system thanger will make it the most easy to access and keep together for everybody. So I dropped all of my current sections into the wiki. I cleaned up the first one a little, so it's now wiki-formatted, instead of LaTeX, and was working on the second section when I realized that I could just make this part of the editing they're supposed to do anyway :) Give them some experience using wikis. I may do a quick tutorial in class at some point, if we've got time. I'll aim to get first drafts of the remaining sections written quickly, so that students can start editing and writing problems and things when we get back from break.
I decided that since there are 5-6 chapters, depending on how I organize things, for the problem/solution writing portion of the project, they can just write one problem/solution per chapter. I'll have to decide how to organize who does solutions for which problems, but I figure I've got a little time in that regard.
For the mini projects, I decided to make them write a (brief, informal) proposal for what they want to do. I made it due next week, which gives me a week to look at them during break (while I'm grading exams, writing the remaining sections, oh, and that thesis thing...). I'm guessing there will be some overlap among projects, so they might end up getting grouped. And it will hopefully give me a chance to make sure everybody is doing "enough", or at least comparable amounts. I told them if they had "big" ideas, and people to work with, their mini project could be in groups. There might be some students who don't want to come up with anything - I told them they'd be assigned a project (possibly just writing more problems/solutions).
When I get carried away, I dream that this project could all come together to something beautiful and useful by the end of the semester (I think some students may be thinking like this too!). That maybe the department would start using it. That maybe folks outside of the department could get something out of it. In the discussions in class, I've told them how I think it would be great to release it as a fairly open project, like under a permissive creative commons license. In class today, I told them to assume they're working on a project that will be released fairly openly, and that if they were opposed to this they should email me or send anonymous feedback. They can still work on things and get their grade, I just wouldn't include their work in a release version (kinda tricky for "editing"... I'm hoping this doesn't come up). I also told them that I wasn't sure what the University would think about such a project, or about such a project being released however we want. Maybe they'll claim it, or restrict how we can distribute it. I'm probably going to go for a "beg forgiveness" approach, instead of "ask permission". I took a quick look online, but didn't find anything about university policies that seemed applicable. Presumably I'm being irresponsible... it's not the first time.
So, anyway. Could be fun. Could be disappointing. Will almost certainly be more work than I've considered. Hopefully we make something useful...
If you've got comments, feedback, or suggestions, I'd love to hear it. I'm sorta making this all up as I go. If you'd like to pre-order your copy today... :) I jest. Mostly. (drop a comment, you might inspire my class)
Saturday, September 4, 2010
Choose Life. Choose a Job. Choose a Career.
This is my last semester as a graduate student, I'm moving on to a "real job." I may graduate. I may not. I basically don't care much either way, at this point. My job offer doesn't depend on my having a Ph.D., and I don't see a future for myself where a Ph.D. is required. Perhaps I'll get fired in short order and will have neither a Ph.D. nor experience/recommendation. I'll cross that bridge if I come to it. I'll feel bad if I don't get my advisor a thesis after all he's done, but hopefully if that happens he'll at least be closer to a paper.
This summer I did an internship as a software developer at Rosetta Stone, where I had a great time. I was on a team full of good people, all easy to work with (the impression I got was that such people were all over the place at Rosetta Stone). During this time I worked on an Adobe AIR application described by my boss at an executive-summary level as a "Fancy Tape Recorder." There was already some work done on it when I came in and, with my fellow intern, I think we got things to a pretty reasonable state by the end of the summer.
I enjoyed my time at Rosetta Stone, and the team I was on seemed to think I was doing good work. At the end of the summer, I submitted an application for full-time employment, and eventually an offer was extended to me. In the mean time, I had also applied to Telogis Research, in New Zealand. I would have gone in a heartbeat, but apparently didn't do well enough on my phone interview. Ah well. At least I had fun with their quiz. The third and final place I applied was CCRi, here in Charlottesville.
After a terribly uncertain week, with lots of lying in bed pondering and not being able to fall asleep, and some last minute craziness (apologies to all involved), I'm finally sorted. CCRi gave an offer I'm pretty excited about, and so I'm going to see what happens there.
I'm quite nervous about it, to be honest, and that's why I was leaning to Rosetta Stone for a while. At CCRi, I'll be a systems engineer. I don't even exactly know what that is. I don't remember the last class I was in that had much to do with applications. As they pointed out during my interview, they've got a lot they need me to learn. I hope I wasn't too far off in my claim that after all this time in school, as student and as teacher, I can learn quickly and effectively. If not, I'm potentially looking at that no job + no phd bridge in short order.
Additionally, I'll need to get a security clearance. Hopefully not much of an issue, but it will mean giving up being an Australian citizen, apparently. And I just got my passport :-(. Ah well. It's been pointed out to me that there are plenty of nice places in the States to live. And it's not like I couldn't go visit. And, since Telogis didn't take me, how likely was it I was heading that way soon anyway? Life was bound to get in the way sooner or later. Still, it's a bummer dude.
So I'm not sure what will happen with this blog. My math fork is already a bit neglected. I guess this has always just been a personal ranting blog anyway, so probably it'll stick around. As this is my last semester teaching, I probably won't have too much more to say about textbooks or institutionalized education (maybe just a little bit as the semester rolls on :)). I'll keep my eye on the space, and I do believe there will be interesting developments there in the next few years (they're happening already). But for now, it looks like I'm out. Off to other things.
Choose rottin' away at the end of it all...
Monday, August 23, 2010
New Homework
I'm thinking about trying something new with homework this semester. The goal is to have students evaluate their own understanding, and have each individual decide how much they need to do in order to attain the understanding they desire. So each week I will tell them to work on particular sections. What they will turn in to me will be something like the following
- I attempted problems: (list of problems)
- Overall (or perhaps per section), I would rate my understanding at: (letter)
- I had the following minor issues: (list of problem with issue, things like... algebra/computational mistake, counting mistake,...)
- I had larger issues with: (list of problems, with work, and a description of the issue - couldn't start, got so far but didn't know what to do next, finished but got the wrong answer and don't understand why)
- Here's a well-written (sentences, little algebra) solution to problem X: (well-written solution).
As far as grading goes, I will probably do something like check for completion - is the student showing me evidence that they are thinking about the problems outside of class? Perhaps I'll use a 0 (didn't turn anything in), 1 (didn't spend more than 5 minutes on what they turned in), 2 (gave it an honest attempt).
There's certainly lots of potential for students to not take this seriously. To some extent, I'm willing to let them, basically. If they choose to not think about the course material, they can see what happens when an exam comes. If they do fine on the exam, so be it. I'm not here to do much for the students who don't need me for help (ok, whatever, I should try to challenge everybody?). I could also use quizzes to see if students claimed understanding is accurate.
So we'll see how that goes, I guess.
Sunday, August 15, 2010
Netflix History
I'm in my 6th straight year of my Netflix subscription. I decided to see my complete history, and found that I've gotten approximately 600 movies through Netflix. A quick average tells me that's 100 movies each year, or about 1 movie every 3.5 days. That's nearly turn-around time for mailing movies. Since I'm currently on the 1-at-a-time, 2-per-month plan, I was kinda surprised. But I guess that's how averages go. In my most prolific month, I returned 20 movies. I was probably on the 5-at-a-time plan then.
Not that it's particularly useful, but I made a chart with the google chart api, showing (to first approximation) the number of movies I got each month. Basically I love coming up with excuses to play with the chart api. Anyway, here it is (even if some of the alignment isn't exactly right):
Not that it's particularly useful, but I made a chart with the google chart api, showing (to first approximation) the number of movies I got each month. Basically I love coming up with excuses to play with the chart api. Anyway, here it is (even if some of the alignment isn't exactly right):
Thursday, August 5, 2010
Colorado Hiking
Just got back from a great hiking trip in Colorado. I got to go with my best friend, Peter, whose parents live near Boulder and were great to us (Thanks you two!). It even sounds like they might not mind if I go back next year! Sweet!
We arrived in Denver in the late evening on Friday, and I don't remember doing much before bedtime. All of the evenings were pretty relaxed, sitting around eating and drinking, wandering around whichever town we were in at the time. Combined with hiking and running, there probably aren't many better ways to spend your time (though, of course, some dawdling around online doesn't hurt).
Saturday we woke up and Peter took me for a run of a few miles, to start getting used to altitude. Peter always kicks my ass running, and makes it look easy. I'm just happy he'll humor me with a run occasionally. It was a fairly flat route (east of the "Front Range", everything is pretty flat), but I certainly remember one hill (which might not even qualify as such in Charlottesville) in particular, and trying to catch my breath for a while. After we got back, we (me, Peter, and his dad, Gary - the same combo for all the hikes) headed out to NCAR (National Center for Atmospheric Research) for a hike up Bear's Peak. Actually, we were going to do South Boulder Peak, but there was maybe some map mis-reading, and it was on the other side of what we were anticipating, I guess. Still, it was a fun hike. Scrambling up rocks, lots of nice views, and more getting used to altitude. It was a... 6ish, let's say, mile hike with something like 2000' elevation gain, ending up in the 9000s. Good times. This was also our only hike without rain.
Sunday we got up and headed out past Rollinsville along a 7 mile or so dirt road to the trailhead for a hike up to Heart Lake. I think this hike came in closer to 8 miles, started around 9k, and finished up around 11k ft or so. I could be mistaken. It was a much easier, technically, hike than Bear's Peak, and gorgeous. Maybe someday I'll be in shape and go back to run the road and also the trail. Someday. Around the time we got the top, it started to drizzle, and it just kept raining harder the whole way down. By the end it was pouring, and lightning was getting pretty close (2 one-thousand ish). I regretted not bringing more of a change of clothes (or leaving clothes in the car - my pack wasn't exactly waterproof), but once Peter sorted out the heat in the car, things were looking better. We stopped in Rollinsville looking for a cup of coffee, but didn't have much luck. We did, however, catch guys with pistols and shotguns standing around the parking lot (we're talking right outside the store) shooting at birds. I don't think I'd last long in Rollinsville on my own. We drove to Nederlands for coffee, and it seemed like a cool little place.
Monday we took it pretty easy. Another half hour run with Peter, and his dad this time, to start the day, then we headed out to Golden (where Coors is made, or so), Red Rocks, and some nearby dinosaur tracks. I think it was this day that I started noticing more how brown everything was. Not that there's anything wrong with that, it's just a change from Virginia (I guess that's sorta part of the point of travel, huh? the change?). Apparently at Red Rocks people like to exercise, among all the stairs. You can run back and forth along the rows of seats; apparently getting 4 miles in without hardly changing your geographical coordinates. Watching everybody, I got pretty tempted to just try bounding up the rows of the stadium. Eventually I decided on a 'next time' approach. After all, we were resting up for our big hike the next day, Long's Peak.
Monday night we went to bed early. It's what you gotta do when you're going to wake up at 1 in the morning. Out the door at 1:30, then a bit of a drive, and on the trail by 3am. This out and back hike is something like 15 miles with 5000' of elevation change, ending above 14000'. Long's Peak, I hear, is the only "14er" in the Rocky Mountain National Park. I also hear it's one of, if not the most, hiked 14er (at least, the Keyhole route that we took), but that only 3 in 10 who try it successfully summit.
So anyway, starting at 3am, there's not much to see for a while. Just hiking along with headlamps on, seeing the first 20 feet, or whatever, of trees on either side of the trail. When we popped out above the tree line, it was still dark. However, the moon was half-full (half-empty?), and I found that it provided plenty of light to see by. We had a gorgeous view of the stars, and even saw a few shooting stars. I was feeling a little dizzy, and couldn't decide if it was the altitude or possibly just something strange with walking with your main light source being a headlamp. I felt a little better when I turned of my headlamp, but the dizzy didn't entirely go away. Probably I just started focusing even more on walking and staying upright, and didn't have as much time to notice the dizzy.
The keyhole route has a handful of landmarks. After you get above the tree line (a bit further than that, even), you come to a Boulder Field, where people camp, and there's some toilets. There are also marmots - always handy to have around for a Lebowski reference. From here you can see the summit basically (though not the route you'll take to get there), and the Keyhole. After the Keyhole comes, if I remember correctly, the Ledge (across, scary), the Trough (up, scary), the Narrows (across, scary), and the Homestretch (up, scary). You'll notice a theme here. At several points I considered telling Peter and his dad I was just going to sit tight and wait for them on their way back down. I kept plodding along though, happy to tell anybody who asked that I was terrified. Peter was worried I was getting mad at him for "making" me do this, but I was far to scared for that. And also too scared to notice much trouble with the elevation. Sure, I got out of breath, but not too bad.
You're welcome to call me a wuss, I don't care. I was scared. Death was quite honestly a possibility (indeed, it has happened to many on this mountain). All it would have taken was one wrong step. I wondered if there was any way I'd be able to catch Peter's (or his dad's) arm if he fell. Lacking anything like upper-body strength, I knew it wouldn't go well. We're all glad it didn't come to that.
We made it to the top around 8:30am. I sat around telling Peter and his dad that there was no way off this rock besides a helicopter. And I wasn't sure they'd be able to make it that high. Eventually (9ish) they decided it was time to head down. "Just take it easy, slide down on your butt", I was told. Of course, everything I know (nothing) says that sliding is exactly what you don't want to do. Despite all of my fears, down was, quite honestly, easier. I'm not here to ponder why (and why would you listen to me anyway?), but it was. Still scary, of course, but manageable.
We were back in the Boulder Field around noon, but decided (mostly) to not stop for lunch because the clouds were clearly starting to form. We wondered a little how the rest of the hike would go for the lady who happily professed that she was "Too f*ing old for this s*" when we passed her on our way down and her way up. Or the couple with their infant (seriously). I hardly wanted to be up there when the clouds weren't there. Perhaps lacking the panoramic view of everything (the cliff a step away) makes it easier, but I doubt it.
As we descended, I was looking forward to getting pictures of the "Alpine fields" we had walked through in the dark, and the forest further down. But right behind us was a rapidly growing, and darkening, storm cloud. Our pace quickened. And paused so we could take pictures, or just gaze around, check our packs for... whatever. And then quickened some more as the lightning and thunder built up. We were still above the tree line (and 2.5ish miles from the parking lot). While I appreciated being tall and lanky during other parts of the hike (scrambling over boulders and trying to make my way up the mountain), I no longer appreciated being the tallest thing around. Peter was behind me on the trail, so slightly higher still, but that wasn't much help. As we were about getting to the tree line, the hail started. I wondered about tornadoes, but couldn't quite believe they'd occur "at elevation". The lightning was more worrying. Eventually I pulled off the trail underneath a tree and next to a rock. Even after Peter said that's not what you're supposed to do, we stayed for a few moments. People passed us, just ambling down the trail, so we decided to go as well.
Eventually the storm calmed down, and I could start feeling the tired in my legs and feet again. The white of the hail all over the ground made everything fairly pretty, even if it was a little hard to appreciate, being a bit cold and wet. We made it back to the parking area, and changed into dry clothes, by about 3pm - 12 hours, 15 miles, and 5000' of elevation gain after our start. Good times.
When we got back and settled and fed and warm, we all started looking around for articles or trip reports about hikes from the day. Apparently the day we hiked was the 50th anniversary of the first successful summit attempt along a particular route (and by a math Ph.D. no less!). I didn't see many other articles. Now, a few days later, Peter and his dad have found some articles about another hiker who's trip didn't go as well as ours. I hope he recovers quickly. And I hope that everybody else on the mountain that day (and others, of course), made it home safely.
Wednesday was another relaxed day, and the day of my flight home. It didn't seem like the end of my trip, though. The flight was scheduled for 6:10pm departure, with arrival in BWI around midnight. We left at least an hour and a half late, due to weather, and got to Baltimore around 1:30am. Then the drive to Peter's place, and I was probably in bed by around 3am. Back up at 5 for work today. I can't say today was my most productive day of programming :) But I did stay awake the whole time, so I consider it a success. And I made it home, and my cats even seem basically happy to see me. So I guess now my trip is done, even if I'm not unpacked.
My pictures are posted (Warmup Hikes and Long's Peak). My memories are written. And my last dose of caffeine is wearing off. So it's bed time.
Some trail wisdom, straight from Sir:
Update 20100807: Peter posted his pictures.
Update 20100808: Gary's pictures and trip report.
We arrived in Denver in the late evening on Friday, and I don't remember doing much before bedtime. All of the evenings were pretty relaxed, sitting around eating and drinking, wandering around whichever town we were in at the time. Combined with hiking and running, there probably aren't many better ways to spend your time (though, of course, some dawdling around online doesn't hurt).
Saturday we woke up and Peter took me for a run of a few miles, to start getting used to altitude. Peter always kicks my ass running, and makes it look easy. I'm just happy he'll humor me with a run occasionally. It was a fairly flat route (east of the "Front Range", everything is pretty flat), but I certainly remember one hill (which might not even qualify as such in Charlottesville) in particular, and trying to catch my breath for a while. After we got back, we (me, Peter, and his dad, Gary - the same combo for all the hikes) headed out to NCAR (National Center for Atmospheric Research) for a hike up Bear's Peak. Actually, we were going to do South Boulder Peak, but there was maybe some map mis-reading, and it was on the other side of what we were anticipating, I guess. Still, it was a fun hike. Scrambling up rocks, lots of nice views, and more getting used to altitude. It was a... 6ish, let's say, mile hike with something like 2000' elevation gain, ending up in the 9000s. Good times. This was also our only hike without rain.
Sunday we got up and headed out past Rollinsville along a 7 mile or so dirt road to the trailhead for a hike up to Heart Lake. I think this hike came in closer to 8 miles, started around 9k, and finished up around 11k ft or so. I could be mistaken. It was a much easier, technically, hike than Bear's Peak, and gorgeous. Maybe someday I'll be in shape and go back to run the road and also the trail. Someday. Around the time we got the top, it started to drizzle, and it just kept raining harder the whole way down. By the end it was pouring, and lightning was getting pretty close (2 one-thousand ish). I regretted not bringing more of a change of clothes (or leaving clothes in the car - my pack wasn't exactly waterproof), but once Peter sorted out the heat in the car, things were looking better. We stopped in Rollinsville looking for a cup of coffee, but didn't have much luck. We did, however, catch guys with pistols and shotguns standing around the parking lot (we're talking right outside the store) shooting at birds. I don't think I'd last long in Rollinsville on my own. We drove to Nederlands for coffee, and it seemed like a cool little place.
Monday we took it pretty easy. Another half hour run with Peter, and his dad this time, to start the day, then we headed out to Golden (where Coors is made, or so), Red Rocks, and some nearby dinosaur tracks. I think it was this day that I started noticing more how brown everything was. Not that there's anything wrong with that, it's just a change from Virginia (I guess that's sorta part of the point of travel, huh? the change?). Apparently at Red Rocks people like to exercise, among all the stairs. You can run back and forth along the rows of seats; apparently getting 4 miles in without hardly changing your geographical coordinates. Watching everybody, I got pretty tempted to just try bounding up the rows of the stadium. Eventually I decided on a 'next time' approach. After all, we were resting up for our big hike the next day, Long's Peak.
Monday night we went to bed early. It's what you gotta do when you're going to wake up at 1 in the morning. Out the door at 1:30, then a bit of a drive, and on the trail by 3am. This out and back hike is something like 15 miles with 5000' of elevation change, ending above 14000'. Long's Peak, I hear, is the only "14er" in the Rocky Mountain National Park. I also hear it's one of, if not the most, hiked 14er (at least, the Keyhole route that we took), but that only 3 in 10 who try it successfully summit.
So anyway, starting at 3am, there's not much to see for a while. Just hiking along with headlamps on, seeing the first 20 feet, or whatever, of trees on either side of the trail. When we popped out above the tree line, it was still dark. However, the moon was half-full (half-empty?), and I found that it provided plenty of light to see by. We had a gorgeous view of the stars, and even saw a few shooting stars. I was feeling a little dizzy, and couldn't decide if it was the altitude or possibly just something strange with walking with your main light source being a headlamp. I felt a little better when I turned of my headlamp, but the dizzy didn't entirely go away. Probably I just started focusing even more on walking and staying upright, and didn't have as much time to notice the dizzy.
The keyhole route has a handful of landmarks. After you get above the tree line (a bit further than that, even), you come to a Boulder Field, where people camp, and there's some toilets. There are also marmots - always handy to have around for a Lebowski reference. From here you can see the summit basically (though not the route you'll take to get there), and the Keyhole. After the Keyhole comes, if I remember correctly, the Ledge (across, scary), the Trough (up, scary), the Narrows (across, scary), and the Homestretch (up, scary). You'll notice a theme here. At several points I considered telling Peter and his dad I was just going to sit tight and wait for them on their way back down. I kept plodding along though, happy to tell anybody who asked that I was terrified. Peter was worried I was getting mad at him for "making" me do this, but I was far to scared for that. And also too scared to notice much trouble with the elevation. Sure, I got out of breath, but not too bad.
You're welcome to call me a wuss, I don't care. I was scared. Death was quite honestly a possibility (indeed, it has happened to many on this mountain). All it would have taken was one wrong step. I wondered if there was any way I'd be able to catch Peter's (or his dad's) arm if he fell. Lacking anything like upper-body strength, I knew it wouldn't go well. We're all glad it didn't come to that.
We made it to the top around 8:30am. I sat around telling Peter and his dad that there was no way off this rock besides a helicopter. And I wasn't sure they'd be able to make it that high. Eventually (9ish) they decided it was time to head down. "Just take it easy, slide down on your butt", I was told. Of course, everything I know (nothing) says that sliding is exactly what you don't want to do. Despite all of my fears, down was, quite honestly, easier. I'm not here to ponder why (and why would you listen to me anyway?), but it was. Still scary, of course, but manageable.
We were back in the Boulder Field around noon, but decided (mostly) to not stop for lunch because the clouds were clearly starting to form. We wondered a little how the rest of the hike would go for the lady who happily professed that she was "Too f*ing old for this s*" when we passed her on our way down and her way up. Or the couple with their infant (seriously). I hardly wanted to be up there when the clouds weren't there. Perhaps lacking the panoramic view of everything (the cliff a step away) makes it easier, but I doubt it.
As we descended, I was looking forward to getting pictures of the "Alpine fields" we had walked through in the dark, and the forest further down. But right behind us was a rapidly growing, and darkening, storm cloud. Our pace quickened. And paused so we could take pictures, or just gaze around, check our packs for... whatever. And then quickened some more as the lightning and thunder built up. We were still above the tree line (and 2.5ish miles from the parking lot). While I appreciated being tall and lanky during other parts of the hike (scrambling over boulders and trying to make my way up the mountain), I no longer appreciated being the tallest thing around. Peter was behind me on the trail, so slightly higher still, but that wasn't much help. As we were about getting to the tree line, the hail started. I wondered about tornadoes, but couldn't quite believe they'd occur "at elevation". The lightning was more worrying. Eventually I pulled off the trail underneath a tree and next to a rock. Even after Peter said that's not what you're supposed to do, we stayed for a few moments. People passed us, just ambling down the trail, so we decided to go as well.
Eventually the storm calmed down, and I could start feeling the tired in my legs and feet again. The white of the hail all over the ground made everything fairly pretty, even if it was a little hard to appreciate, being a bit cold and wet. We made it back to the parking area, and changed into dry clothes, by about 3pm - 12 hours, 15 miles, and 5000' of elevation gain after our start. Good times.
When we got back and settled and fed and warm, we all started looking around for articles or trip reports about hikes from the day. Apparently the day we hiked was the 50th anniversary of the first successful summit attempt along a particular route (and by a math Ph.D. no less!). I didn't see many other articles. Now, a few days later, Peter and his dad have found some articles about another hiker who's trip didn't go as well as ours. I hope he recovers quickly. And I hope that everybody else on the mountain that day (and others, of course), made it home safely.
Wednesday was another relaxed day, and the day of my flight home. It didn't seem like the end of my trip, though. The flight was scheduled for 6:10pm departure, with arrival in BWI around midnight. We left at least an hour and a half late, due to weather, and got to Baltimore around 1:30am. Then the drive to Peter's place, and I was probably in bed by around 3am. Back up at 5 for work today. I can't say today was my most productive day of programming :) But I did stay awake the whole time, so I consider it a success. And I made it home, and my cats even seem basically happy to see me. So I guess now my trip is done, even if I'm not unpacked.
My pictures are posted (Warmup Hikes and Long's Peak). My memories are written. And my last dose of caffeine is wearing off. So it's bed time.
Some trail wisdom, straight from Sir:
It's always raining somewhere.Take it easy.
Update 20100807: Peter posted his pictures.
Update 20100808: Gary's pictures and trip report.
Tuesday, May 11, 2010
Super Troopers
Super Troopers is one of my favorite movies. At some point recently I decided it was time to watch the Broken Lizard collection again. Then a friend pointed out their most recent just came out. So it's been a good time for movies recently.
As I was sitting down to watch Super Troopers, I thought up a fun project: try to pick a single frame "for" the movie. I haven't really been able to further describe what I mean... "advertising" the movie doesn't quite cut it, nor does "capturing", entirely. But something like that. So I pulled out a couple, and thought I'd share them. That's what the ends of semesters are for, right? Movies? I guess exam time was always Dr. Mario time when I was a student...
I've put a good line with most of the frames. It's not always the line going on in the frame, but it's nearby.
A friend who has seen the movie many times (perhaps not particularly recently) suggested the following from memory:
"Do we look like the two dumbest guys in the world to you?"
Another friend, who hasn't seen it quite so frequently, picked out the following scene (I grabbed what seemed a good frame to me):
"Good enough for me!"
There's a lot of magic in the first scene, but I'm not sure I found a particularly great frame. From it, I picked out:
"What'd you say man?"
Of course, one of the most-quoted lines, I expect comes at the burger joint:
"I don't want a large Farva."
But a good frame should probably be a little independent of the lines it suggests. There's a fair amount of humor tucked in this frame, but it might be a bit buried:
"Ten deep breaths, I got it 'cap."
This one's a little bit more obviously funny:
"Okee silly dilly dokey oh, I'm an idiot."
As is this one:
"Finish it up, rook."
I also like frames with the group, in uniform, but not looking particularly official, like:
"It's really funny 'cap. It's Afghanistanimation."
or
"Maybe we should take another look."
I think if somebody made me pick a single frame, it might just be this last one.
Apparently my point is you should probably just go watch it. And maybe let me know what frame(s) you'd pick.
As I was sitting down to watch Super Troopers, I thought up a fun project: try to pick a single frame "for" the movie. I haven't really been able to further describe what I mean... "advertising" the movie doesn't quite cut it, nor does "capturing", entirely. But something like that. So I pulled out a couple, and thought I'd share them. That's what the ends of semesters are for, right? Movies? I guess exam time was always Dr. Mario time when I was a student...
I've put a good line with most of the frames. It's not always the line going on in the frame, but it's nearby.
A friend who has seen the movie many times (perhaps not particularly recently) suggested the following from memory:
"Do we look like the two dumbest guys in the world to you?"
Another friend, who hasn't seen it quite so frequently, picked out the following scene (I grabbed what seemed a good frame to me):
"Good enough for me!"
There's a lot of magic in the first scene, but I'm not sure I found a particularly great frame. From it, I picked out:
"What'd you say man?"
Of course, one of the most-quoted lines, I expect comes at the burger joint:
"I don't want a large Farva."
But a good frame should probably be a little independent of the lines it suggests. There's a fair amount of humor tucked in this frame, but it might be a bit buried:
"Ten deep breaths, I got it 'cap."
This one's a little bit more obviously funny:
"Okee silly dilly dokey oh, I'm an idiot."
As is this one:
"Finish it up, rook."
I also like frames with the group, in uniform, but not looking particularly official, like:
"It's really funny 'cap. It's Afghanistanimation."
or
"Maybe we should take another look."
I think if somebody made me pick a single frame, it might just be this last one.
Apparently my point is you should probably just go watch it. And maybe let me know what frame(s) you'd pick.
Finishing Up
Still have one student that needs to take a make-up final, but I'm basically done for the semester. I all honesty, I probably checked out a few weeks ago. I've got something like a vaguely un-scheduled week ahead of me (besides a Flying Karamazov Brothers show!), until a math conference in Georgia in the second half of next week. People tell me it'll be good to go. That remains to be seen. And basically as soon as I get back, I start a summer programming internship at Rosetta Stone. Could be something. So with my loose week, I just gotta bang out a thesis so I don't have to come back in the fall...
Err, right. So this post was supposed to be about thoughts about my class this semester. Things that went well (it ended). Things that went poorly (the other parts). Things to do differently next time (next time‽). Something I can look back on in the fall for guidance.
So... reading assignments with homework due before we talked about it in class didn't go hugely well. I stand by the method. But I've also been reading about how homework itself, as a graded assignment, sucks (maybe start at joebower.org if you want to follow along at home), so I'm a little torn. Halfway through the semester I switched to the following setup: read the book for Tuesday, and submit a "discussion seed" based on the reading, as your homework assignment for Tuesday. I then used the those discussion seeds as what I brought up in class Tuesday, and then had written problems due Thursday. Seemed to go fairly ok, as a setup. Basing class time on questions students had actually submitted seemed like sort of a fun idea. Having the questions as a Google Docs presentation seemed to work ok.
My students really seemed intrigued when I showed actual housing cost data, so I should work to bring more actual data into my classroom. I was also thinking it might be cool to have guest speakers, maybe from banking or realty. Perhaps I'll look into that more for next semester. Probably the best thing about this class is that students can actually mostly see it as something useful. Putting money in an account, saving up... sorta easy to relate to, I think. There's some amount of intrinsic motivation there, if I can just capture it.
One important thing I didn't know going in to the semester was what sorts of students took the course. It's a 100-level course; I was expecting mostly freshman and sophomores. No dice. Probably half of my class was graduating seniors, many of whom already probably knew basically all of the material. I sorta have a hard time believing these students should actually be allowed to take this course... this is part of the stupid game I hate about education when I think about it these days. I had friends in undergrads who, as graduating actuarial science seniors, took 100-level "finite math" sorts of classes. This seems like what sorta happened with the class I taught this semester. The impression I get is that many of them were then upset with the class for being boring. What the hell do you want from me? Other students, in the last few days, have mentioned that they thought I did well trying to balance for these students along with those who actually didn't know much of the material coming in. I think it helps that mostly the students who didn't need to be there stopped showing up.
Another thing I didn't know coming in was the content of the course. I was reading the book along with the students. Turns out, there's very little material. In a few-minute wrapup I did on the last day, I told my students how essentially we did one thing all semester: move money around on a timeline. Compound interest is just iterated simple interest. Bank discount interest is just simple interest from a different perspective. Annuities formulas are just conveniences for dealing with many things moving around at compound interest. And that's all we did. I'm a little curious to see if I could teach all of the formulas in a week or two. Knowing this, I intend to go faster next semester and cover more material. I think this should help with some of the boredom issue.
I'm toying with the idea of using next semester, when I'll likely be teaching the course again, as a chance to have the students write their own textbook. There were enough errors and oddities in the textbook we did use, I have a hard time believing we couldn't do better. We'll do a big collaborative project, as the entire class, writing a book. I think a project like this could be good for having students involved and interested. I also think it should be a good way for students to learn the material - you learn best by teaching. And, finally, I think we could make a pretty decent book.
Each semester we math grad students are given a teaching request form, where we get to request what to teach the following semester. Basically it's one of the four calculus sections (two levels of calc 1 and calc 2), and then occasionally this financial math course, or a calc 3. On my form, I requested to teach this financial math class again. A friend thought I was joking when I told her. My advisor asked if I was a masochist. I think, having gone through it once, the next time can't help but go better, which will be nice. I know the material now, and might not be quite as caught off guard by my class being mostly seniors. Also, the class has no emphasis on algebra, my current frustration with calculus courses. I do need to try to design better assignments that have students explain their work more, but hopefully I can sort something out. Writing a book should be good for that.
Anyway, I'm off. Take 'er easy.
Err, right. So this post was supposed to be about thoughts about my class this semester. Things that went well (it ended). Things that went poorly (the other parts). Things to do differently next time (next time‽). Something I can look back on in the fall for guidance.
So... reading assignments with homework due before we talked about it in class didn't go hugely well. I stand by the method. But I've also been reading about how homework itself, as a graded assignment, sucks (maybe start at joebower.org if you want to follow along at home), so I'm a little torn. Halfway through the semester I switched to the following setup: read the book for Tuesday, and submit a "discussion seed" based on the reading, as your homework assignment for Tuesday. I then used the those discussion seeds as what I brought up in class Tuesday, and then had written problems due Thursday. Seemed to go fairly ok, as a setup. Basing class time on questions students had actually submitted seemed like sort of a fun idea. Having the questions as a Google Docs presentation seemed to work ok.
My students really seemed intrigued when I showed actual housing cost data, so I should work to bring more actual data into my classroom. I was also thinking it might be cool to have guest speakers, maybe from banking or realty. Perhaps I'll look into that more for next semester. Probably the best thing about this class is that students can actually mostly see it as something useful. Putting money in an account, saving up... sorta easy to relate to, I think. There's some amount of intrinsic motivation there, if I can just capture it.
One important thing I didn't know going in to the semester was what sorts of students took the course. It's a 100-level course; I was expecting mostly freshman and sophomores. No dice. Probably half of my class was graduating seniors, many of whom already probably knew basically all of the material. I sorta have a hard time believing these students should actually be allowed to take this course... this is part of the stupid game I hate about education when I think about it these days. I had friends in undergrads who, as graduating actuarial science seniors, took 100-level "finite math" sorts of classes. This seems like what sorta happened with the class I taught this semester. The impression I get is that many of them were then upset with the class for being boring. What the hell do you want from me? Other students, in the last few days, have mentioned that they thought I did well trying to balance for these students along with those who actually didn't know much of the material coming in. I think it helps that mostly the students who didn't need to be there stopped showing up.
Another thing I didn't know coming in was the content of the course. I was reading the book along with the students. Turns out, there's very little material. In a few-minute wrapup I did on the last day, I told my students how essentially we did one thing all semester: move money around on a timeline. Compound interest is just iterated simple interest. Bank discount interest is just simple interest from a different perspective. Annuities formulas are just conveniences for dealing with many things moving around at compound interest. And that's all we did. I'm a little curious to see if I could teach all of the formulas in a week or two. Knowing this, I intend to go faster next semester and cover more material. I think this should help with some of the boredom issue.
I'm toying with the idea of using next semester, when I'll likely be teaching the course again, as a chance to have the students write their own textbook. There were enough errors and oddities in the textbook we did use, I have a hard time believing we couldn't do better. We'll do a big collaborative project, as the entire class, writing a book. I think a project like this could be good for having students involved and interested. I also think it should be a good way for students to learn the material - you learn best by teaching. And, finally, I think we could make a pretty decent book.
Each semester we math grad students are given a teaching request form, where we get to request what to teach the following semester. Basically it's one of the four calculus sections (two levels of calc 1 and calc 2), and then occasionally this financial math course, or a calc 3. On my form, I requested to teach this financial math class again. A friend thought I was joking when I told her. My advisor asked if I was a masochist. I think, having gone through it once, the next time can't help but go better, which will be nice. I know the material now, and might not be quite as caught off guard by my class being mostly seniors. Also, the class has no emphasis on algebra, my current frustration with calculus courses. I do need to try to design better assignments that have students explain their work more, but hopefully I can sort something out. Writing a book should be good for that.
Anyway, I'm off. Take 'er easy.
Monday, April 19, 2010
Teaching
I've started thinking that, perhaps, I don't actually enjoy teaching. Which is to say, there seems to be quite a bit about being a teacher that I really don't care for. Or I'm doing it wrong. Perhaps this is just how it all goes... nothing's perfect, right?
I love learning (my own, I'm not sure I can sense others'). I love reading. I think I enjoy meeting with individuals, or with small groups, who are truly motivated to learn something that I can help with. Not motivated in the sense of finishing an assignment, but in understanding material for understanding-sake. Perhaps it's content I already know, or something I can join them in learning. That might just be where my joy in teaching ends. Sadly, this doesn't seem like much of what school is (or, like I said, I'm doing it wrong).
I want to help individuals learn something that they are interesting in learning. I have no interest in talking to a classroom full of students about things few of them care about. I have no interest in trying to motivate them to care. I have a hard enough time with my own motivation to encourage others in that regard. And, looking back, I know that when I was a student, I didn't care about most of my classes, and don't expect I was interested in being told I should care. I didn't try to learn the material for its intrinsic value. This is especially true outside of math and computer science, but I expect even in some of those classes I was just getting through assignments (at least sometimes). Now that I'm about done with taking school, I'm finally ready to learn just about anything.
Probably I should just suck it up. There are always at least a few students who are paying attention, who are learning something, right? I should focus on them, right? I should figure out how to make things so exciting that people just can't help themselves but want to learn? I should continue giving homework and exams and playing the grading game, without it helping my students much at all. I should humor the notion, hinted at by award nominations, that I'm a "good teacher", despite knowing that I'm hardly doing anybody much good.
I should continue playing this game.
But I think I've realized about myself that I don't like other people's games. I like my own games. I think I might go find some of those...
I love learning (my own, I'm not sure I can sense others'). I love reading. I think I enjoy meeting with individuals, or with small groups, who are truly motivated to learn something that I can help with. Not motivated in the sense of finishing an assignment, but in understanding material for understanding-sake. Perhaps it's content I already know, or something I can join them in learning. That might just be where my joy in teaching ends. Sadly, this doesn't seem like much of what school is (or, like I said, I'm doing it wrong).
I want to help individuals learn something that they are interesting in learning. I have no interest in talking to a classroom full of students about things few of them care about. I have no interest in trying to motivate them to care. I have a hard enough time with my own motivation to encourage others in that regard. And, looking back, I know that when I was a student, I didn't care about most of my classes, and don't expect I was interested in being told I should care. I didn't try to learn the material for its intrinsic value. This is especially true outside of math and computer science, but I expect even in some of those classes I was just getting through assignments (at least sometimes). Now that I'm about done with taking school, I'm finally ready to learn just about anything.
Probably I should just suck it up. There are always at least a few students who are paying attention, who are learning something, right? I should focus on them, right? I should figure out how to make things so exciting that people just can't help themselves but want to learn? I should continue giving homework and exams and playing the grading game, without it helping my students much at all. I should humor the notion, hinted at by award nominations, that I'm a "good teacher", despite knowing that I'm hardly doing anybody much good.
I should continue playing this game.
But I think I've realized about myself that I don't like other people's games. I like my own games. I think I might go find some of those...
Monday, April 5, 2010
A Smile
As my amused smile
turned full-face grin
staring at my plate
I hated her for making it so
I couldn't look up
I knew I'd see
Her smile.
Her eyes on mine.
His smile.
It's ok to smile
I told myself
and never came
her sass about it
The mistakes I've made.
=========
Sorry usual readers. Back to my usual confused rants with the next post, surely. I reckon this one at least fits the "confused" trend.
turned full-face grin
staring at my plate
I hated her for making it so
I couldn't look up
I knew I'd see
Her smile.
Her eyes on mine.
His smile.
It's ok to smile
I told myself
and never came
her sass about it
The mistakes I've made.
=========
Sorry usual readers. Back to my usual confused rants with the next post, surely. I reckon this one at least fits the "confused" trend.
Friday, March 19, 2010
Textbooks
(begin rant)
Two days ago, an email went around the math department here indicating that the higher ups were thinking about changing calculus textbooks, and that there would be a meeting today to talk about it. The meeting was essentially a presentation from a salesman from the textbook company about how great the new textbook is. A few minutes of discussion before-hand, and a comment that those making the change (I'm pretty sure it's a foregone conclusion) would hear our thoughts on the matter. I sorta felt, leaving the meeting, that we'd get a somewhat formal (at least an email) request for comments. Now, a few hours later, I'm guessing we wont. In fact, they probably just signed a contract while the guy was here today.
Sorry, I'm a bit cynical.
Before I go on, I'm probably supposed to make some disclosures. I have at times made (and am currently making) money doing things associated with the Webwork online homework system (admin, library tending). I grew up on Stewart's textbook (used it as a student, and it's what UVA has been using since before I got here). The textbook we are thinking about switching to (like, apparently, everybody else considering switching textbooks) is Briggs and Cochran. At the meeting today, I got a free copy. They also gave us an access code to their online software, MyMathLab.
In all fairness, the new book looks fine. It looks like basically every other recently-released calculus textbook I've looked at (don't take that to mean I've looked at a lot, of for large amounts of time). There are lots of pretty pictures, and apparently the author(s) are big on geometric intuition, which is great. We were also told to be impressed that in the worked examples, each step was given a little explanation. And, gosh, isn't this something amazing, the authors organized the problems at the end of each section carefully. We were told several times that this was not a lower level book, clearly something the publishers are worried about people thinking. It is, as @MitchKeller opined about the projects it has, "a bit hand-holdy".
Oh, and there'll be a new edition along every 3 years.
Of course, the textbook by itself isn't, I expect, what people are all giddy about. The textbook is paired up with MyMathLab. You can make online homework assignments and quizzes. There are little tools for the students to use to get help, like looking at worked examples, looking at a digital copy of the textbook, and probably some others I forgot. Students can also see a little "Study Guide", a sort of summary of what sorts of problems they missed, so they would know what to go back and look at. Oh, and some large collection of those pretty pictures in the text are pretty animations (calculus being about change, we were reminded by the salesman) in the MyMathLab system.
Students have the option to not buy the physical book (at least, in theory, who knows what our goofy school will require), and instead spend somewhat less and just use the e-book in MyMathLab. I seem to recall the e-book being in the $70 range, the first year textbook in the $90s, and the 3 semester book in the $130s, +$6 for the MyMathLab software if you buy the textbook. These numbers might all be before bookstore markup (we were also told to be pleased that the UVA bookstore markup of ~25% is really low... go team!), and we were told that these prices are cheaper than Stewart. The presenter today did this cute thing where he pretended not to already know the price of the books, and looked them up online.
Digital rights management didn't really come up at the meeting today, and I'm ashamed that I didn't bring it up.
Quite honestly, it seems like a not entirely bad thing. Switching textbooks isn't the worst thing we could do. Like I said on twitter after the meeting, though, it feels like shuffling deck chairs on the Titanic.
If I were given freedom to set up the course however I wanted, I wouldn't require that my students purchase this, or any other, textbook. There are simply too many free resources online for me to justify requiring students to spend that money. If students want to buy the book, or the software (more accurately: access (likely temporary) to it), good for them. Go for it. But if a student would rather use their brother's old textbook, say, or the free ones they find online, that's fine too. If instructors are going to lecture (I generally do, more than I'd like), many students can likely get by on class notes (their own, or a friend's), maybe in combination with some office hours.
Sure, the pictures in the book were nice. And the animations. But there are plenty of calculus animations online (I'm not gonna google that for you). In fact, I could roll my own (and have, happily), and would be delighted to teach students to do so as well. It'd be awesome to talk to students about pictures during class, draw them on the board, and then have them make a digital version of the picture, or an animation (for the ambitious) (and release them all under a CC license, wouldn't that be a fun thing to talk about in class). Heck, why not have the calc students write a book, complete with pictures? Write about the things they got hung up on, and what got them over it. Make a wiki. The instructor likely has access to several textbooks. Use them to put together an outline for the semester. Lecture if you want, or tell them to go see what they can learn online or at the library (then use class time to synthesize what was found). Looking up resources online, you also get to talk about evaluating resources, and how to compare different sources. You can build up a big huge list, and have students rate each source (and share your result with... everybody!).
And as for step-by-step explanations, WolframAlpha jumps to mind, but there are certainly others (I'm not gonna google that for you either). Don't like W|A's solution to a problem (they can be a bit... pedantic)? Have students talk about improvements. This also points out that those problems are pointless anyway. A computer does them more quickly and more accurately, so let it. Let's work on understanding concepts, instead of continuing to test pointless algebra tricks. Use the time that we're not doing mechanical manipulations to come to the geometric understanding slowly, guiding students to discover it for themselves.
Webwork has, for me, done a perfectly adequate job as an online homework system. If UVA doesn't think the problem library is nice enough, of the interface good enough, perhaps they should invest some money in improving it (I know they (at least, Dr. Jeff Holt, through a grant) have to some extent, and also that there is money floating around). Then even more people benefit (webwork is open source), and UVA gets some nice credibility. Webwork can do most of the things the guy today tried to sell us on for online assignments, though it's interface might not be as gosh durn pretty. It will not show students which section from the book they missed problems on (it's not tied to any one book). But I don't really see the problem here. I think it would be a great exercise to teach students how to evaluate for themselves which sections they need to look at.
I know I'm not going on much but youthful optimism and naivety. It's not the first time, nor likely the last. I have no expectation at all that the powers that be will take my thoughts seriously. At least here I can pretend that my thoughts are worthwhile (thanks Blogger). I'm leaving after next year anyway, and have seen no evidence (I suppose I haven't asked) that the younger grad students think like I do. I should probably just let it go (until I'm at another school). [As I was writing this post, I decided to email the math grads, to see if they'd like more flexibility in their teaching.]
All I want is for the department to allow instructors to try something different. Let us not require our students to purchase the (any) textbook. Get out of the publisher's pointless "new edition" cycle
Think about dropping the heavy emphasis on algebra.
(end rant (for now))
Two days ago, an email went around the math department here indicating that the higher ups were thinking about changing calculus textbooks, and that there would be a meeting today to talk about it. The meeting was essentially a presentation from a salesman from the textbook company about how great the new textbook is. A few minutes of discussion before-hand, and a comment that those making the change (I'm pretty sure it's a foregone conclusion) would hear our thoughts on the matter. I sorta felt, leaving the meeting, that we'd get a somewhat formal (at least an email) request for comments. Now, a few hours later, I'm guessing we wont. In fact, they probably just signed a contract while the guy was here today.
Sorry, I'm a bit cynical.
Before I go on, I'm probably supposed to make some disclosures. I have at times made (and am currently making) money doing things associated with the Webwork online homework system (admin, library tending). I grew up on Stewart's textbook (used it as a student, and it's what UVA has been using since before I got here). The textbook we are thinking about switching to (like, apparently, everybody else considering switching textbooks) is Briggs and Cochran. At the meeting today, I got a free copy. They also gave us an access code to their online software, MyMathLab.
In all fairness, the new book looks fine. It looks like basically every other recently-released calculus textbook I've looked at (don't take that to mean I've looked at a lot, of for large amounts of time). There are lots of pretty pictures, and apparently the author(s) are big on geometric intuition, which is great. We were also told to be impressed that in the worked examples, each step was given a little explanation. And, gosh, isn't this something amazing, the authors organized the problems at the end of each section carefully. We were told several times that this was not a lower level book, clearly something the publishers are worried about people thinking. It is, as @MitchKeller opined about the projects it has, "a bit hand-holdy".
Oh, and there'll be a new edition along every 3 years.
Of course, the textbook by itself isn't, I expect, what people are all giddy about. The textbook is paired up with MyMathLab. You can make online homework assignments and quizzes. There are little tools for the students to use to get help, like looking at worked examples, looking at a digital copy of the textbook, and probably some others I forgot. Students can also see a little "Study Guide", a sort of summary of what sorts of problems they missed, so they would know what to go back and look at. Oh, and some large collection of those pretty pictures in the text are pretty animations (calculus being about change, we were reminded by the salesman) in the MyMathLab system.
Students have the option to not buy the physical book (at least, in theory, who knows what our goofy school will require), and instead spend somewhat less and just use the e-book in MyMathLab. I seem to recall the e-book being in the $70 range, the first year textbook in the $90s, and the 3 semester book in the $130s, +$6 for the MyMathLab software if you buy the textbook. These numbers might all be before bookstore markup (we were also told to be pleased that the UVA bookstore markup of ~25% is really low... go team!), and we were told that these prices are cheaper than Stewart. The presenter today did this cute thing where he pretended not to already know the price of the books, and looked them up online.
Digital rights management didn't really come up at the meeting today, and I'm ashamed that I didn't bring it up.
Quite honestly, it seems like a not entirely bad thing. Switching textbooks isn't the worst thing we could do. Like I said on twitter after the meeting, though, it feels like shuffling deck chairs on the Titanic.
If I were given freedom to set up the course however I wanted, I wouldn't require that my students purchase this, or any other, textbook. There are simply too many free resources online for me to justify requiring students to spend that money. If students want to buy the book, or the software (more accurately: access (likely temporary) to it), good for them. Go for it. But if a student would rather use their brother's old textbook, say, or the free ones they find online, that's fine too. If instructors are going to lecture (I generally do, more than I'd like), many students can likely get by on class notes (their own, or a friend's), maybe in combination with some office hours.
Sure, the pictures in the book were nice. And the animations. But there are plenty of calculus animations online (I'm not gonna google that for you). In fact, I could roll my own (and have, happily), and would be delighted to teach students to do so as well. It'd be awesome to talk to students about pictures during class, draw them on the board, and then have them make a digital version of the picture, or an animation (for the ambitious) (and release them all under a CC license, wouldn't that be a fun thing to talk about in class). Heck, why not have the calc students write a book, complete with pictures? Write about the things they got hung up on, and what got them over it. Make a wiki. The instructor likely has access to several textbooks. Use them to put together an outline for the semester. Lecture if you want, or tell them to go see what they can learn online or at the library (then use class time to synthesize what was found). Looking up resources online, you also get to talk about evaluating resources, and how to compare different sources. You can build up a big huge list, and have students rate each source (and share your result with... everybody!).
And as for step-by-step explanations, WolframAlpha jumps to mind, but there are certainly others (I'm not gonna google that for you either). Don't like W|A's solution to a problem (they can be a bit... pedantic)? Have students talk about improvements. This also points out that those problems are pointless anyway. A computer does them more quickly and more accurately, so let it. Let's work on understanding concepts, instead of continuing to test pointless algebra tricks. Use the time that we're not doing mechanical manipulations to come to the geometric understanding slowly, guiding students to discover it for themselves.
Webwork has, for me, done a perfectly adequate job as an online homework system. If UVA doesn't think the problem library is nice enough, of the interface good enough, perhaps they should invest some money in improving it (I know they (at least, Dr. Jeff Holt, through a grant) have to some extent, and also that there is money floating around). Then even more people benefit (webwork is open source), and UVA gets some nice credibility. Webwork can do most of the things the guy today tried to sell us on for online assignments, though it's interface might not be as gosh durn pretty. It will not show students which section from the book they missed problems on (it's not tied to any one book). But I don't really see the problem here. I think it would be a great exercise to teach students how to evaluate for themselves which sections they need to look at.
I know I'm not going on much but youthful optimism and naivety. It's not the first time, nor likely the last. I have no expectation at all that the powers that be will take my thoughts seriously. At least here I can pretend that my thoughts are worthwhile (thanks Blogger). I'm leaving after next year anyway, and have seen no evidence (I suppose I haven't asked) that the younger grad students think like I do. I should probably just let it go (until I'm at another school). [As I was writing this post, I decided to email the math grads, to see if they'd like more flexibility in their teaching.]
All I want is for the department to allow instructors to try something different. Let us not require our students to purchase the (any) textbook. Get out of the publisher's pointless "new edition" cycle
Think about dropping the heavy emphasis on algebra.
(end rant (for now))
Wednesday, March 10, 2010
Thoughts on "Dehumanized"
You should go read "Dehumanized: When math and science rule the school." Even if you've read it before, and even if it was recently, go read it again. Perhaps a few times.
In this essay, Mark Slouka expresses disappointment that education is being "retooled... into an adjunct of business" at the expense of the arts and humanities.
This is certainly a fair thing to be disappointed about.
I've never really been "in to" the humanities. I don't remember ever much caring about my history classes, or social studies. I don't think I took many literature classes, and can't say I feel like I got much out of any that I did take. I blame nobody but myself, of course. While reading "Dehumanized" I became convinced that I have seriously missed out. It's sad that now, age 26, supposedly 1 year away from a Ph.D., I'm finally ready to go to school.
I do not agree with everything in the article, though. Throughout, Slouka seems to wish that civics were the highest goal of education. I'm not sure I see why this should be. Of course, I'm pretty sure I don't even know "what" this would be, so I don't have much basis for argument. But I think many of the goals Slouka advocates, with the apparent intention of improving individuals as citizens, are goals I do agree with.
Slouka asks, "What do we teach, and why?" Clearly a fantastic question. He even provides some answers: "whatever contributes to the development of autonomous human beings", "in order to expand the census of knowledgeable, reasoning, independent-minded individuals." I like those answers, even if Slouka seems to want these things for the purpose of "the political life of the nation." I guess I feel like I want these things for the individual, and those around the individual. Perhaps that's what politics is/are. I don't know, I probably wasn't paying attention that day.
The humanities, it is claimed, are there to talk about "what it means to be fully human," to teach "not what to do but how to be". The output is "the reasoned search for truth." But then Slouka says these things are all, "inescapably, political." Perhaps the reasons why all point out why I don't know what "political" means: "they complicate our vision", "grow uncertainty", "expand the reach of our understanding" (and thus "compassion" and "tolerance"). One goal seems to be "an individual formed through questioning". The de-toothing of humanities education is summarized:
The arts and humanities are there to "upset people", prompt "unscripted, unapproved questions", and, according to Don Randel, "force us into 'a rigorous cross-examination of our myths about ourselves'". Slouka quotes the teacher Marcus Eure who wants students to have "depth of experience and a willingness to be wrong", and notes that "every aspect of life... hinges in some way on the ability to understand and empathize with others, to challenge one's belief, to strive for reason and clarity."
These all sound like awesome things.
What confuses me about the article is that the author doesn't seem to think math and science help with these goals. I just don't see that at all. Uncertainty? Understanding? Questioning? Cross-examination? Reason and clarity? How are those not in the realm of math and science? Sure, the topics that are questioned and reasoned about are different for mathandscience than for the humanities, as it pointed out by the article. But how can the questioning nature of mathandscience, the logic and reasoning, not be helpful in the humanities? Is it because math and science education, in parallel to education in the humanities, isn't what it really could and should be? Of course, having also just re-read "A Mathematician's Lament", I worry that this is quite likely the case. But that's probably the topic for another day.
In this essay, Mark Slouka expresses disappointment that education is being "retooled... into an adjunct of business" at the expense of the arts and humanities.
This is certainly a fair thing to be disappointed about.
I've never really been "in to" the humanities. I don't remember ever much caring about my history classes, or social studies. I don't think I took many literature classes, and can't say I feel like I got much out of any that I did take. I blame nobody but myself, of course. While reading "Dehumanized" I became convinced that I have seriously missed out. It's sad that now, age 26, supposedly 1 year away from a Ph.D., I'm finally ready to go to school.
I do not agree with everything in the article, though. Throughout, Slouka seems to wish that civics were the highest goal of education. I'm not sure I see why this should be. Of course, I'm pretty sure I don't even know "what" this would be, so I don't have much basis for argument. But I think many of the goals Slouka advocates, with the apparent intention of improving individuals as citizens, are goals I do agree with.
Slouka asks, "What do we teach, and why?" Clearly a fantastic question. He even provides some answers: "whatever contributes to the development of autonomous human beings", "in order to expand the census of knowledgeable, reasoning, independent-minded individuals." I like those answers, even if Slouka seems to want these things for the purpose of "the political life of the nation." I guess I feel like I want these things for the individual, and those around the individual. Perhaps that's what politics is/are. I don't know, I probably wasn't paying attention that day.
The humanities, it is claimed, are there to talk about "what it means to be fully human," to teach "not what to do but how to be". The output is "the reasoned search for truth." But then Slouka says these things are all, "inescapably, political." Perhaps the reasons why all point out why I don't know what "political" means: "they complicate our vision", "grow uncertainty", "expand the reach of our understanding" (and thus "compassion" and "tolerance"). One goal seems to be "an individual formed through questioning". The de-toothing of humanities education is summarized:
Worried about indoctrination, we've short-circuited argument. Fearful of propoganda, we've taken away the only tools that could detect and counter it.
The arts and humanities are there to "upset people", prompt "unscripted, unapproved questions", and, according to Don Randel, "force us into 'a rigorous cross-examination of our myths about ourselves'". Slouka quotes the teacher Marcus Eure who wants students to have "depth of experience and a willingness to be wrong", and notes that "every aspect of life... hinges in some way on the ability to understand and empathize with others, to challenge one's belief, to strive for reason and clarity."
These all sound like awesome things.
What confuses me about the article is that the author doesn't seem to think math and science help with these goals. I just don't see that at all. Uncertainty? Understanding? Questioning? Cross-examination? Reason and clarity? How are those not in the realm of math and science? Sure, the topics that are questioned and reasoned about are different for mathandscience than for the humanities, as it pointed out by the article. But how can the questioning nature of mathandscience, the logic and reasoning, not be helpful in the humanities? Is it because math and science education, in parallel to education in the humanities, isn't what it really could and should be? Of course, having also just re-read "A Mathematician's Lament", I worry that this is quite likely the case. But that's probably the topic for another day.
Thursday, February 11, 2010
Project Wrapup
I want to share my thoughts on how my recent in-class project went. Basically I still think it's a reasonable project. It certainly needs some tweaking though. I'm kinda excited to try it again.
Recap
Class began and I started as close to on time as possible. I had already posted the assignment, and some students had seen it. I did a quick run-through of the setup, explaining the two parts (write your own problems, with solutions, and solve a different groups problems). As students divided themselves into groups I distributed printed copies of the assignment. Students got in and settled and started working pretty quickly, which was nice. Throughout, it seemed like students were doing a reasonable job staying focus on the task. I think the time pressure helps with that.
I let students work without any interruption for a few minutes. One student came to me and asked if the problem he had written was ok. It looked quite similar to textbook problems, which I told him, and he went away a bit disappointed. After a few minutes I started wandering around to each group, asking how things were going. Many of the groups were perfectly happy, and didn't have any questions for me. A few groups were having a hard time coming up with things. I tried to indicate how one might make up a new problem. For example, make up crazy rules a bank might use for some sort of account. Or: look at a textbook problem. They solve an equation for one of the 4 variables in our formula. Change the problem around so that a different variable is the one to be found. Sometimes this might not make a particularly new problem, but I think sometimes it could. The students I gave these suggestions to seemed to think they could make progress, and got back to work.
A few other students showed me problems that looked like textbook problems. One told me that it was different, and I challenged him to explain how. He noted that his problem tested the interpretation of the answers from some textbook questions. I can't really argue. He had 3 problems, 2 of which looked like textbook problems, and the third asked for the interpretation. Fair enough I guess.
At the half-hour mark, when students were supposed to be done writing problems, nobody was. I talked to them about it, and it was pointed out that probably solving problems that are already written would be quicker than writing your own. So the second half should go quicker. Makes sense. I told them all to take 15 more minutes on writing their own questions and solutions.
Just after the first group finished, it occurred to me that I should emphasize that they are all getting the same grade. So they should make sure to double check each other's work. I think many groups were divvying up work, so that each person wrote a solution to one problem. This is fine, but I think it is important that all of the group members double-check this work too. I made an announcement about this.
We were running out of time. With 25 minutes, groups were mostly starting to finish, and I re-distributed problems to groups that were done the first part. Since the time wasn't working out as I had anticipated, I told them to solve 2 of the 4 problems they were given.
With about 15 minutes to go, all but 2 groups had begun the second part of the assignment, solving another groups problems. One of the two remaining groups finished (group A), and the other was done 3 of 4 problems (group B). I took the 3 problems over to the group A to start the second part, but let group B continue working on their own problems. Group A eventually finished, about 5 minutes over time, and group B didn't have any time to work on group A's problems when they had finished writing their own. I'm still trying to decide what to do about that. [I assigned them some of the more challenging problems I had written]
While students were working on problems other groups had written, I decided it might be interesting to have them rate the creativity of the problems they were given. I told them to rate each problem they were given with either a 0 (this is a textbook problem), 1 (kinda new), or 2 (terribly interesting). I'm not sure how seriously they took this task, I have not yet (as I write this), looked at the work that was turned in. [Mostly I think this turned out ok, though some 2's were pretty questionable]
As students were finishing, I told them (a) I wanted feedback on the project, what they liked/disliked, how it could have been better, and (b) that I'd probably like to try this again, so to keep track of questions they think of outside of class.
After Class
I've been trying to write daily (we only meet twice a week) blog posts for my class, on whatever we talked about that day. I don't think any of the students are reading them, but I could be wrong. Today I posted questions I had dreamt up, to give students some sort of idea what I had in mind. Some of the questions I had though up before class, others were inspired by discussion in class.
As I was writing up my questions, it occurred to me that several of them weren't quite as original as I had originally (bam!) thought. I could see how to translate my problems into textbook problems. I do still feel like there would be a translation step though, and I guess that's part of the game. Or perhaps I'm fooling myself.
I emailed the class, specifically encouraging them to read my post, and also to provide feedback. Hopefully the reminder generates some feedback.
Initial Reaction
I mis-judged timing. I had originally given more time for doing other groups problems than writing one's own. Definitely backwards. Probably we could do 45 minutes writing problems, and 30 answering others'. Also, I think I need to be firm on the deadline if I try this again. At 45 minutes, you will have to give me your paper, and will lose points for not having written enough problems (well, you just don't earn the points you would have). Of course, that means the group that gets your paper isn't being graded out of as many problems, which must be accounted for. Hmmm.
I think trying this again, students may have a better sense about the project. Writing problems might come easier. Hopefully, then, timing would work out a little better. Perhaps showing students a list of questions before-hand would have been a good idea.
I didn't plan enough about organizing the work that got turned in. I'm sort of dreading looking at the pile. Here's how I think I'd organize it next time: Each group is assigned a number. There are then 4 things they turn in to me by the end of class:
I sorta like the idea of getting students to rate the problems they are given for creativity. I can't quite decide what to do about giving points based on those ratings, as they'd be pretty easily gamed. One option I came up with: Have students rate the problems they were given on the 0-2 scale above. As I'm grading, type up all the problems that earned a 2. Distribute this list, without any identifying marks, back to the students, and have them pick their favorite n, say (outlawing voting for your own (more bookkeeping for me, but doable as long as I have them write their name on the paper)). Any problem that gets more than m "favorites" earns the authoring group p points (1, likely).
Grading
As I organized papers, and got to a point I could start grading, I realized that I could extend this project to have the students do the grading. Group A gives their answers to Group B, and when Group B is done, Group A grades the solutions. This could be a valuable exercise for the students, seeing how their questions were interpreted, perhaps seeing other ways to solve questions they had designed. Of course, it leads to problems about what grade gets written down in the grade book... suggestions?
As I was grading, I realized that students can game the grading system by writing easy questions. This guarantees 3 points for solutions to each problem the group writes, even if they lose a point or two for writing uninteresting problems (I was pretty relaxed about taking points off for this). Perhaps this can be corrected for by having other groups rate "originality" first, (maybe "difficulty" too) and then base the score solutions are worth out of that grade?
Maybe take interesting problems in to class, have everybody do them, and talk about answers. Also problems with difficult wording.
On re-distributing papers: Group A did Group B's problems. Giving A's solutions back to A, they probably won't be able to see B's questions, to look back at.
Student Feedback
At this point, I still haven't gotten much. One said they enjoyed the project, even if making up problems was difficult. Another suggested just writing up questions individually and exchanging papers with partners; that working in larger groups was hard. Also the timing issues were pointed out.
Current Thoughts for Next Time
Be more organized about what names I need to see on which papers. I found that the paper-shuffling aspect of grading was easier for groups where group A did group B's problems and vice-versa. I'm not sure that it matters too much though.
Perhaps break this project into two class period. In the first, groups will meet to try to create interesting problems that they could solve (though I won't ask for solutions just yet). The problems will be re-distributed around the room, and groups will rate the originality and difficulty of the problems they were given. I will then gather up all of the problems, and we'll end class. Before the next class, I'll go through all the problems, find all those that earned good originality/difficulty ratings, and compile them into a list. In class the next time, all of the students will work those problems, maybe just working with a neighbor. Then we can spend time in class discussing solutions to the problems, talking about different interpretations of questions, what makes questions well-written, etc. There's issues here about turning in solutions - if students just wait until we talk about solutions in class, they can just copy those.
Thoughts?
I'd really like to know what you think about any or all of this. I know it's rather a lot to read through, sorry.
Recap
Class began and I started as close to on time as possible. I had already posted the assignment, and some students had seen it. I did a quick run-through of the setup, explaining the two parts (write your own problems, with solutions, and solve a different groups problems). As students divided themselves into groups I distributed printed copies of the assignment. Students got in and settled and started working pretty quickly, which was nice. Throughout, it seemed like students were doing a reasonable job staying focus on the task. I think the time pressure helps with that.
I let students work without any interruption for a few minutes. One student came to me and asked if the problem he had written was ok. It looked quite similar to textbook problems, which I told him, and he went away a bit disappointed. After a few minutes I started wandering around to each group, asking how things were going. Many of the groups were perfectly happy, and didn't have any questions for me. A few groups were having a hard time coming up with things. I tried to indicate how one might make up a new problem. For example, make up crazy rules a bank might use for some sort of account. Or: look at a textbook problem. They solve an equation for one of the 4 variables in our formula. Change the problem around so that a different variable is the one to be found. Sometimes this might not make a particularly new problem, but I think sometimes it could. The students I gave these suggestions to seemed to think they could make progress, and got back to work.
A few other students showed me problems that looked like textbook problems. One told me that it was different, and I challenged him to explain how. He noted that his problem tested the interpretation of the answers from some textbook questions. I can't really argue. He had 3 problems, 2 of which looked like textbook problems, and the third asked for the interpretation. Fair enough I guess.
At the half-hour mark, when students were supposed to be done writing problems, nobody was. I talked to them about it, and it was pointed out that probably solving problems that are already written would be quicker than writing your own. So the second half should go quicker. Makes sense. I told them all to take 15 more minutes on writing their own questions and solutions.
Just after the first group finished, it occurred to me that I should emphasize that they are all getting the same grade. So they should make sure to double check each other's work. I think many groups were divvying up work, so that each person wrote a solution to one problem. This is fine, but I think it is important that all of the group members double-check this work too. I made an announcement about this.
We were running out of time. With 25 minutes, groups were mostly starting to finish, and I re-distributed problems to groups that were done the first part. Since the time wasn't working out as I had anticipated, I told them to solve 2 of the 4 problems they were given.
With about 15 minutes to go, all but 2 groups had begun the second part of the assignment, solving another groups problems. One of the two remaining groups finished (group A), and the other was done 3 of 4 problems (group B). I took the 3 problems over to the group A to start the second part, but let group B continue working on their own problems. Group A eventually finished, about 5 minutes over time, and group B didn't have any time to work on group A's problems when they had finished writing their own. I'm still trying to decide what to do about that. [I assigned them some of the more challenging problems I had written]
While students were working on problems other groups had written, I decided it might be interesting to have them rate the creativity of the problems they were given. I told them to rate each problem they were given with either a 0 (this is a textbook problem), 1 (kinda new), or 2 (terribly interesting). I'm not sure how seriously they took this task, I have not yet (as I write this), looked at the work that was turned in. [Mostly I think this turned out ok, though some 2's were pretty questionable]
As students were finishing, I told them (a) I wanted feedback on the project, what they liked/disliked, how it could have been better, and (b) that I'd probably like to try this again, so to keep track of questions they think of outside of class.
After Class
I've been trying to write daily (we only meet twice a week) blog posts for my class, on whatever we talked about that day. I don't think any of the students are reading them, but I could be wrong. Today I posted questions I had dreamt up, to give students some sort of idea what I had in mind. Some of the questions I had though up before class, others were inspired by discussion in class.
As I was writing up my questions, it occurred to me that several of them weren't quite as original as I had originally (bam!) thought. I could see how to translate my problems into textbook problems. I do still feel like there would be a translation step though, and I guess that's part of the game. Or perhaps I'm fooling myself.
I emailed the class, specifically encouraging them to read my post, and also to provide feedback. Hopefully the reminder generates some feedback.
Initial Reaction
I mis-judged timing. I had originally given more time for doing other groups problems than writing one's own. Definitely backwards. Probably we could do 45 minutes writing problems, and 30 answering others'. Also, I think I need to be firm on the deadline if I try this again. At 45 minutes, you will have to give me your paper, and will lose points for not having written enough problems (well, you just don't earn the points you would have). Of course, that means the group that gets your paper isn't being graded out of as many problems, which must be accounted for. Hmmm.
I think trying this again, students may have a better sense about the project. Writing problems might come easier. Hopefully, then, timing would work out a little better. Perhaps showing students a list of questions before-hand would have been a good idea.
I didn't plan enough about organizing the work that got turned in. I'm sort of dreading looking at the pile. Here's how I think I'd organize it next time: Each group is assigned a number. There are then 4 things they turn in to me by the end of class:
- The list of problems they wrote. This should have "Written by group N" on it. It should also have "Solved by group M", the group that gets these problems.
- The list of solutions to their own problems. This should have "Written by group N" on it.
- The list of solutions to the problems they were given. This should have "Solutions written by group N, for group M's problems" on it. These solutions should not be on the same paper with the questions, since it mucks up re-distributing papers (more on this below).
- A paper with the group number and names of all of the group members. I suppose this information could just go on, say, the list of solutions a group writes for their own problems
I sorta like the idea of getting students to rate the problems they are given for creativity. I can't quite decide what to do about giving points based on those ratings, as they'd be pretty easily gamed. One option I came up with: Have students rate the problems they were given on the 0-2 scale above. As I'm grading, type up all the problems that earned a 2. Distribute this list, without any identifying marks, back to the students, and have them pick their favorite n, say (outlawing voting for your own (more bookkeeping for me, but doable as long as I have them write their name on the paper)). Any problem that gets more than m "favorites" earns the authoring group p points (1, likely).
Grading
As I organized papers, and got to a point I could start grading, I realized that I could extend this project to have the students do the grading. Group A gives their answers to Group B, and when Group B is done, Group A grades the solutions. This could be a valuable exercise for the students, seeing how their questions were interpreted, perhaps seeing other ways to solve questions they had designed. Of course, it leads to problems about what grade gets written down in the grade book... suggestions?
As I was grading, I realized that students can game the grading system by writing easy questions. This guarantees 3 points for solutions to each problem the group writes, even if they lose a point or two for writing uninteresting problems (I was pretty relaxed about taking points off for this). Perhaps this can be corrected for by having other groups rate "originality" first, (maybe "difficulty" too) and then base the score solutions are worth out of that grade?
Maybe take interesting problems in to class, have everybody do them, and talk about answers. Also problems with difficult wording.
On re-distributing papers: Group A did Group B's problems. Giving A's solutions back to A, they probably won't be able to see B's questions, to look back at.
Student Feedback
At this point, I still haven't gotten much. One said they enjoyed the project, even if making up problems was difficult. Another suggested just writing up questions individually and exchanging papers with partners; that working in larger groups was hard. Also the timing issues were pointed out.
Current Thoughts for Next Time
Be more organized about what names I need to see on which papers. I found that the paper-shuffling aspect of grading was easier for groups where group A did group B's problems and vice-versa. I'm not sure that it matters too much though.
Perhaps break this project into two class period. In the first, groups will meet to try to create interesting problems that they could solve (though I won't ask for solutions just yet). The problems will be re-distributed around the room, and groups will rate the originality and difficulty of the problems they were given. I will then gather up all of the problems, and we'll end class. Before the next class, I'll go through all the problems, find all those that earned good originality/difficulty ratings, and compile them into a list. In class the next time, all of the students will work those problems, maybe just working with a neighbor. Then we can spend time in class discussing solutions to the problems, talking about different interpretations of questions, what makes questions well-written, etc. There's issues here about turning in solutions - if students just wait until we talk about solutions in class, they can just copy those.
Thoughts?
I'd really like to know what you think about any or all of this. I know it's rather a lot to read through, sorry.
Wednesday, February 10, 2010
Approximating Functions of Shapes
Every now and then, I end up writing about my research at a not-too-technical level. Here's my latest attempt:
The branch of mathematics known as topology is concerned with the study of shapes. Whereas shapes in geometry are fairly rigid objects, shapes in topology are much more flexible. If one flexible shape can be flexed and twisted and not-too-drastically mangled into another flexible shape, topology deems them to be the same. It becomes much more difficult, then, to tell if two shapes are different. The question of topology is, ``Given two flexible shapes, how can we tell if they are the same?''
In geometry, much time is spent studying shapes like triangles and quadrilaterals. If you draw one triangle on one sheet of paper, and another triangle on another sheet of paper, then there is an easy way to tell if those two triangles are the same. Namely, shift the papers around, possibly flip one or the other over, rotate them, and see if you can get the triangles to line up. If you can, then the triangles are ``the same'' (congruent). If you can't line up the triangles (and have put forth enough effort), then the triangles are not the same. Similarly, you could draw a square on one paper, a triangle on the other, and try to line those shapes up. Of course, you will never succeed, because the two shapes will always have a different number of sides.
In topology, we might consider the same scenario of triangles and squares, but instead of using ordinary paper, we would draw our shapes on a sheet of flexible rubber (an inflatable balloon, say). Indeed, topology is often referred to as ``rubber-sheet geometry.'' Now that the surface is flexible, by pulling it in the appropriate directions one can get the square to look like a triangle. Or either shape to look like a circle. To a topologist, this means that all of these shapes are ``the same'' (homeomorphic). The topologist still has some rules in place, though. You are not allowed to cut holes in the balloon, or glue parts of the balloon together.
With all of the additional flexibility, we have a harder time telling two shapes apart. We can no longer rely on the number of sides, or the lengths of sides. Other methods must be found.
It turns out that a good way to get a sense of how similar two shapes are is to understand how the shapes are related to yet another shape. Suppose we have two flexible shapes, called Shape 1 and Shape 2. One might try to obtain information about Shape 1 in isolation, and compare that to information obtained about Shape 2 in isolation. However, as the shapes are flexible, there's only so much we can tell by looking at each shape independently. Instead, we introduce another flexible shape, Shape 3. Generally Shape 3 is a shape that has been much studied, like a circle. Now we ask, ``How many ways can Shape 3 be put into Shape 1?'' and, ``How many ways can Shape 3 be put into Shape 2?'' We call a single way of putting Shape 3 into Shape 1, if it is reasonably well-behaved, an ``embedding.'' If the embeddings of Shape 3 into either of the two original Shapes are similar, we might decide that the two shapes themselves are fairly similar. We can then replace Shape 3 with Shape 4, repeat the question, and get an even finer appreciation for how similar Shapes 1 and 2 are.
The entire collection of embeddings of Shape 3 into Shape 1 can all be gathered up and reasonably interpreted as making up yet another shape. However, it can be a fairly difficult shape to get a good sense of. Instead, one might ask if there is a way to approximate this shape. Perhaps an initial approximation can be attained, and then that approximation can be refined, and refined further, giving a better and better understanding of the complicated shape we originally sought. Using geometry as an example, one might approximate a circle by a square, and then refine the approximation to an octagon, and carry on the process of adding more sides to the approximating figure. This was the method used, historically, for calculating the area of a circle.
But the idea of approximating the shape of the collection of embeddings can be further generalized. If we have a strong handle on a particular shape, say S, then our first step in understanding any new shape that comes along might be to find all the ways S can be put into the new shape. We have, then, described a function. Given a shape, X, we can ask for the shape of ways that S can be embedded in X. We might denote this function by E(X), and call it the embedding function for S. Now instead of understanding a particular value, E(X), of this function, we might ask about understanding the function E as a whole. While the function itself is likely complicated, we can try to approximate it, as before.
In my research, I study a family of embeddings functions. The functions are based on the ``Euclidean spaces'' of various dimensions: a point, a line, a plane, three-dimensional space, and on to higher dimensions. From a topologist's perspective, these are the easiest shapes there are, but they can be used to build up nearly all of the other shapes worth studying, so are of fundamental importance. Instead of just thinking about one such space as the basis for my function, I might make a collection of them; say, 3 lines and 2 planes. I only ask about E(X) when X is, itself, a single Euclidean space.
It might seem that by restricting my study to particularly nice shapes S and X, and particularly nice ways to put S into X, I have eliminated any hope of doing anything useful. However, this is not the case. An important class of shapes, called manifolds, are built up from Euclidean spaces by gluing them together. By obtaining a particularly nice description of embedding functions using my restricted shapes S, there are known ways to assemble them into the embedding functions for more general manifolds.
Previous work has found nice ways to describe embedding functions for some of the cases I am considering. If the base space, S, is a finite collection of points, then spaces of embeddings are what are known as ``Configuration Spaces,'' and these detect one type of behavior for embeddings. Alternatively, if S has just a single space, but of any dimension, the spaces of embeddings are detecting a different sort of behavior. Nice descriptions for the embedding functions in both of these cases are known. It has been my task to unify the two descriptions, allowing for an understanding of embedding functions when the known space, S, is a collection of any number of Euclidean spaces.
Update 20100225: There's a somewhat different version of this on my other blog.
The branch of mathematics known as topology is concerned with the study of shapes. Whereas shapes in geometry are fairly rigid objects, shapes in topology are much more flexible. If one flexible shape can be flexed and twisted and not-too-drastically mangled into another flexible shape, topology deems them to be the same. It becomes much more difficult, then, to tell if two shapes are different. The question of topology is, ``Given two flexible shapes, how can we tell if they are the same?''
In geometry, much time is spent studying shapes like triangles and quadrilaterals. If you draw one triangle on one sheet of paper, and another triangle on another sheet of paper, then there is an easy way to tell if those two triangles are the same. Namely, shift the papers around, possibly flip one or the other over, rotate them, and see if you can get the triangles to line up. If you can, then the triangles are ``the same'' (congruent). If you can't line up the triangles (and have put forth enough effort), then the triangles are not the same. Similarly, you could draw a square on one paper, a triangle on the other, and try to line those shapes up. Of course, you will never succeed, because the two shapes will always have a different number of sides.
In topology, we might consider the same scenario of triangles and squares, but instead of using ordinary paper, we would draw our shapes on a sheet of flexible rubber (an inflatable balloon, say). Indeed, topology is often referred to as ``rubber-sheet geometry.'' Now that the surface is flexible, by pulling it in the appropriate directions one can get the square to look like a triangle. Or either shape to look like a circle. To a topologist, this means that all of these shapes are ``the same'' (homeomorphic). The topologist still has some rules in place, though. You are not allowed to cut holes in the balloon, or glue parts of the balloon together.
With all of the additional flexibility, we have a harder time telling two shapes apart. We can no longer rely on the number of sides, or the lengths of sides. Other methods must be found.
It turns out that a good way to get a sense of how similar two shapes are is to understand how the shapes are related to yet another shape. Suppose we have two flexible shapes, called Shape 1 and Shape 2. One might try to obtain information about Shape 1 in isolation, and compare that to information obtained about Shape 2 in isolation. However, as the shapes are flexible, there's only so much we can tell by looking at each shape independently. Instead, we introduce another flexible shape, Shape 3. Generally Shape 3 is a shape that has been much studied, like a circle. Now we ask, ``How many ways can Shape 3 be put into Shape 1?'' and, ``How many ways can Shape 3 be put into Shape 2?'' We call a single way of putting Shape 3 into Shape 1, if it is reasonably well-behaved, an ``embedding.'' If the embeddings of Shape 3 into either of the two original Shapes are similar, we might decide that the two shapes themselves are fairly similar. We can then replace Shape 3 with Shape 4, repeat the question, and get an even finer appreciation for how similar Shapes 1 and 2 are.
The entire collection of embeddings of Shape 3 into Shape 1 can all be gathered up and reasonably interpreted as making up yet another shape. However, it can be a fairly difficult shape to get a good sense of. Instead, one might ask if there is a way to approximate this shape. Perhaps an initial approximation can be attained, and then that approximation can be refined, and refined further, giving a better and better understanding of the complicated shape we originally sought. Using geometry as an example, one might approximate a circle by a square, and then refine the approximation to an octagon, and carry on the process of adding more sides to the approximating figure. This was the method used, historically, for calculating the area of a circle.
But the idea of approximating the shape of the collection of embeddings can be further generalized. If we have a strong handle on a particular shape, say S, then our first step in understanding any new shape that comes along might be to find all the ways S can be put into the new shape. We have, then, described a function. Given a shape, X, we can ask for the shape of ways that S can be embedded in X. We might denote this function by E(X), and call it the embedding function for S. Now instead of understanding a particular value, E(X), of this function, we might ask about understanding the function E as a whole. While the function itself is likely complicated, we can try to approximate it, as before.
In my research, I study a family of embeddings functions. The functions are based on the ``Euclidean spaces'' of various dimensions: a point, a line, a plane, three-dimensional space, and on to higher dimensions. From a topologist's perspective, these are the easiest shapes there are, but they can be used to build up nearly all of the other shapes worth studying, so are of fundamental importance. Instead of just thinking about one such space as the basis for my function, I might make a collection of them; say, 3 lines and 2 planes. I only ask about E(X) when X is, itself, a single Euclidean space.
It might seem that by restricting my study to particularly nice shapes S and X, and particularly nice ways to put S into X, I have eliminated any hope of doing anything useful. However, this is not the case. An important class of shapes, called manifolds, are built up from Euclidean spaces by gluing them together. By obtaining a particularly nice description of embedding functions using my restricted shapes S, there are known ways to assemble them into the embedding functions for more general manifolds.
Previous work has found nice ways to describe embedding functions for some of the cases I am considering. If the base space, S, is a finite collection of points, then spaces of embeddings are what are known as ``Configuration Spaces,'' and these detect one type of behavior for embeddings. Alternatively, if S has just a single space, but of any dimension, the spaces of embeddings are detecting a different sort of behavior. Nice descriptions for the embedding functions in both of these cases are known. It has been my task to unify the two descriptions, allowing for an understanding of embedding functions when the known space, S, is a collection of any number of Euclidean spaces.
Update 20100225: There's a somewhat different version of this on my other blog.
Subscribe to:
Posts (Atom)